Bangun Datar - Poin 100
Keberadaan internet membuat siapa saja bisa mengakses berbagai informasi, maka tidak heran belakangan ini banyak sekali betebaran situs-situs yang membahas mengenai Bangun Datar. Hal ini sangat logis mengingat di era pandemi ini, masyarakat kita lebih sering melakukan proses belajar mengajar secara daring. Baiklah sudah cukup basa-basinya, yuk langsung masuk ke pembahasan saja.
Penjelasan Lengkap Bangun Datar
Berdasarkan yang disebutkan oleh wikipedia, bangun datar merupakan sebutan untuk berbagai bangun dua dimensi.
Bangun datar diantaranya seperti: lingkaran, belah ketupat, layang-layang, trapesium, jajar genjang, segitiga, persegi panjang serta persegi.
Pada tiap-tiap bangun tersebut memiliki rumus untuk menghitung luas sekaligus keliling yang berbeda satu bangun dengan bangun yang lain. Selengkapnya mengenai bidang datar, simak baik-baik ulasan di bawah ini ya.
Bangun Datar
Melengkapi uraian di atas, bangun datar merupakan suatu bagian dari bidang datar yang dibatasi oleh garis-garis lurus atau lengkung.
Definisnya sendiri secara rinci ialah: suatu bangun yang memiliki bidang rata serta mempunyai dua dimensi yakni panjang dan lebar namun tidak mempunyai tinggi dan tebal.
Dengan begitu, pengertian singkatnya dari bangun datar adalah abstrak.
Rumus Bangun Datar
Berikut ini akan kami berikan macam atau jenis dari bangun datar beserta sifatnya. Perhatikan ulasan di bawah ini.
1. Persegi
Pengertian Persegi
Persegi merupakan suatu bangun datar 2 dimensi yang terbentuk oleh 4 buah rusuk dengan memiliki ukuran sama panjang serta memiliki 4 buah sudut siku – siku.
Persegi juga bisa kita sebut sebagai bangun datar yang mempunyai sisi sisi sama panjang serta sudut sudut sama besar.
Sifat Persegi
- Seluruh sisi-sisinya memiliki ukuran panjang yang sama serta seuruh sisinya berhadapan sejajar.
- Masing-masing sudut yang dimilikinya adalah sudut siku-siku.
- Memiliki dua diagonal dengan ukuran panjang yang sama sama serta berpotongan di tengah-tengah dan membentuk sudut siku-siku.
- Pada masing-masing sudutnya di bagi dua sama besarnya oleh diagonalnya.
- Memiliki empat buah sumbu simetri.
Rumus yang ada pada Persegi
Berikut ini adalah beberapa rumus yang biasa digunakan pada bangun persegi, antara lain:
Rumus luas persegi, yaitu:
L = S x S
Rumus keliling persegi, yaitu:
K = S + S + S + S ataupun K = 4 x S
Keterangan:
- L: Luas
- K: Keliling
- S: Sisi
Contoh Soal:
Perhatikanlah gambar di bawah ini:
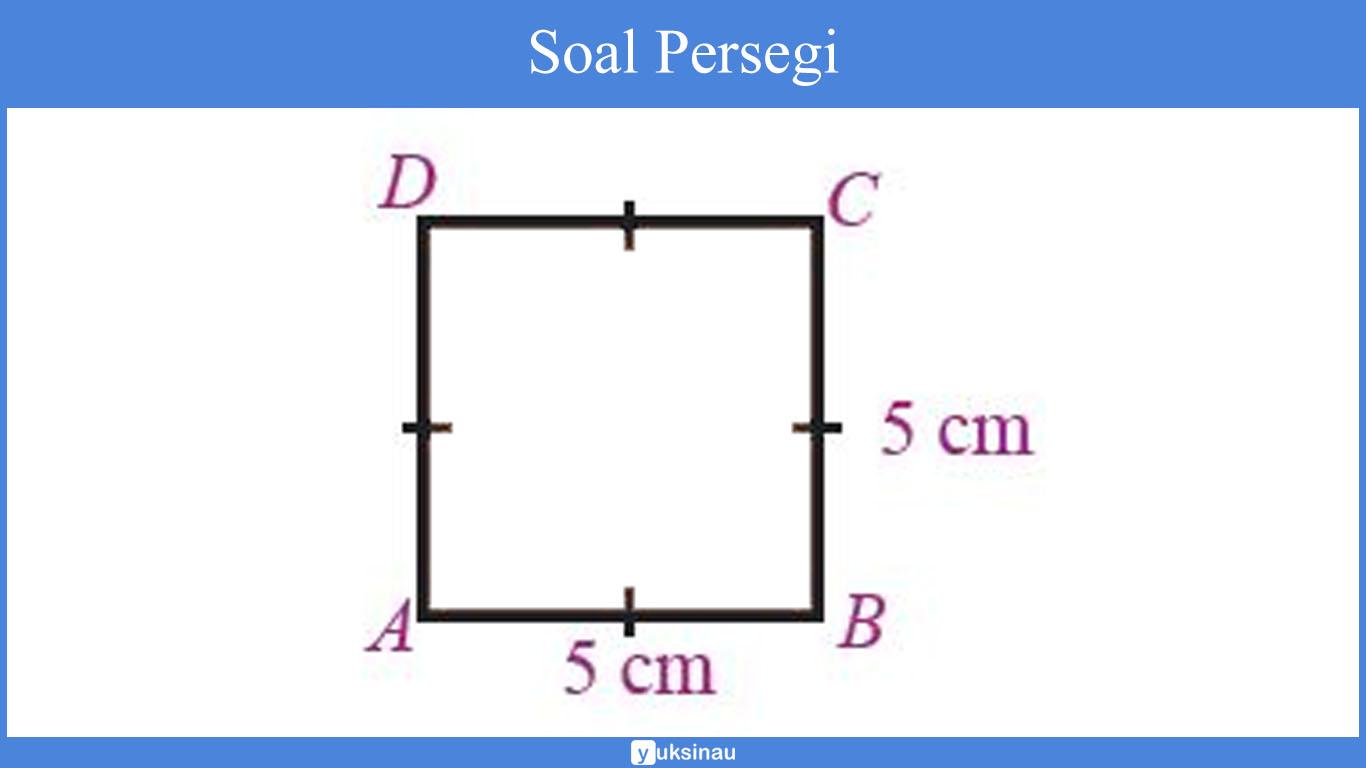
Dari gambar di atas, tentukan:
a. Tentukan luas perseginya:
b. Tentukan keliling perseginya:
Jawab:
a. Rumus Luas persegi ABCD yakni: s x s, sehingga
= 5 cm x 5 cm
= 25 cm2.
Jadi, luas persegi ABCD yaitu: 25 cm2.
b. Rumus Keliling persegi ABCD ialah: 4 x s, sehingga
= 4 x 5 cm
= 20 cm.
Jadi, jumlah keliling persegi ABCD tersebut yaitu 20 cm.
2. Persegi Panjang
Pengertian Persegi Panjang
Persegi panjang meurpakan suatu bangun datar 2 dimensi yang terbentuk oleh 2 buah pasang rusuk yang panjang serta sejajar dan memiliki 4 buah sudut siku – siku.
Sifat Bangun Datar Persegi Panjang
- Masing-masing sisi-sisi yang berhadapan memiliki ukuran sama panjang dan juga sejajar.
- Seluruh sudutnya merupakan sudut siku-siku.
- Mempunyai dua buah diagonal yang sama panjang serta saling berpotongan di titik pusat bangun persegi panjang. Titik tersebut adalah membagi dua bagian diagonal dengan ukuran sama panjang.
- Mempunyai dua buah sumbu simetri yakni sumbu vertikal dan juga sumbu horizontal.
Rumus yang ada pada Bangun Datar Persegi Panjang
Rumus luas persegi panjang, yaitu:
L = p x l
Rumus keliling persegi panjang, yaitu:
K = 2 x (p + l)
Keterangan:
- L: Luas
- K: Keliling
- p: panjang
- l: lebar
Contoh Soal
Suatu bangun persegi panjang, mempunyai p = 10 cm dan l = 5 cm, terdiri atas EFGH:
Pertanyaan:
a. Hitunglah luas persegi panjang EFGH:
b. Hitunglah keliling persegi panjang EFGH!:
Jawab:
a. Rumus luas persegi panjang EFGH adalah L= p x l, sehingga
L = 10 cm x 5 cm
L = 50 cm2.
Jadi, luas persegi panjang EFGH yaitu 50 cm2.
b. Rumus Keliling sama persegi panjang EFGH adalah: 2 x (p + l), sehingga
= 2 x (10 cm + 5 cm)
= 2 x 15 cm.
= 30 cm
Jadi, keliling persegi panjang EFGH yaitu 50 cm.
3. Segitiga
Pengertian Bangun Datar Segitiga
Segitiga merupakan suatu bangun datar 2 dimensi yang dibentuk oleh 3 buah sisi yang berwujud garis lurus serta 3 buah sudut.
Sehingga bangun datar yang terbentuk dari tiga atau lebih garis lurus disebut sebagai segitiga.
Sifat Bangun Datar Segitiga
- Pada bangunan segitiga, ketiga sudutnya memiliki besaran 180º. (jika dijumlahkan hasilnya 180)
- Sifat Segitiga mempunyai 3 sisi serta 3 titik sudut.
Rumus yang ada pada Bangun Datar Segitiga
Rumus luas segitiga yaitu:
Luas = ½ x a x t
Rumus keliling segitiga yaitu:
Keliling = s + s + s atau K = a + b + c
Suatu bangun segitiga memiliki sebuah ukuran seperti yang tertera di gambar di bawah ini:
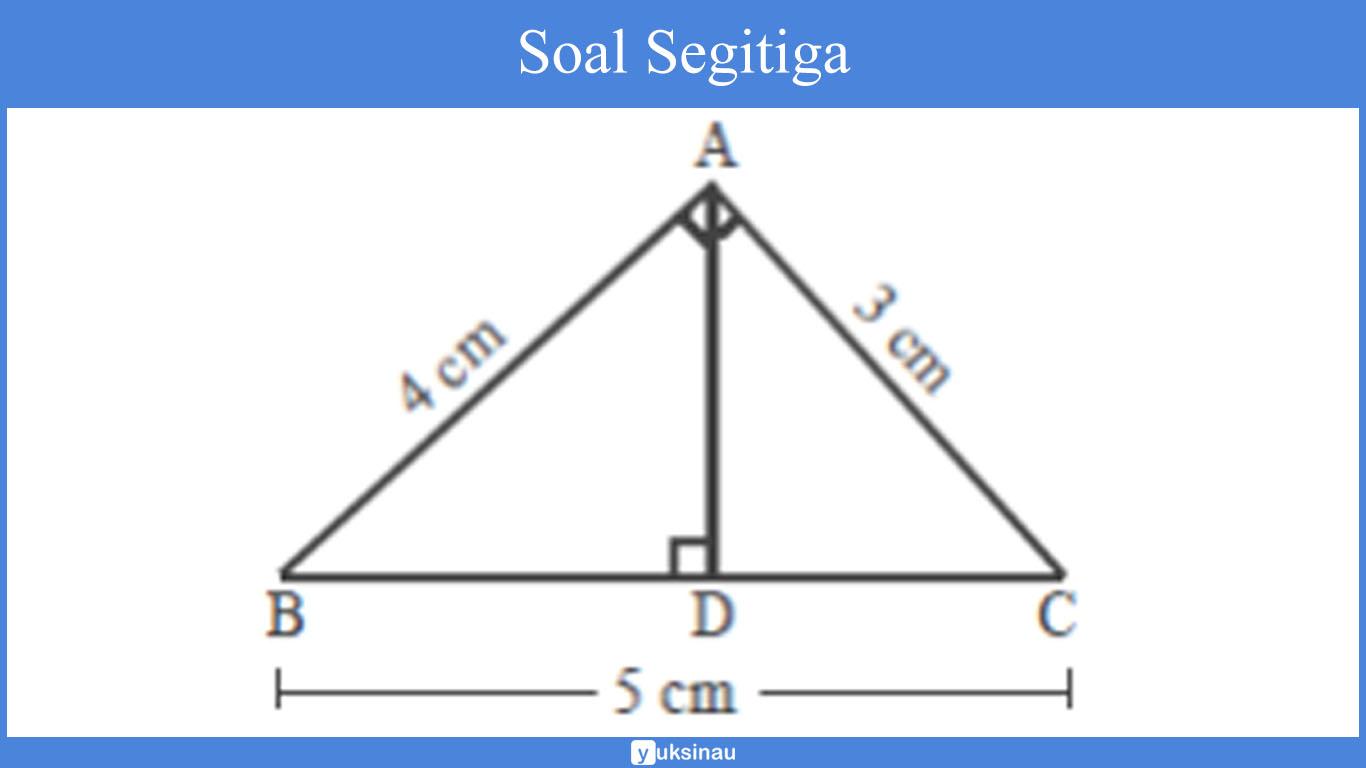
Pertanyaan:
a. Hitunglah luas segitiga :
b. Hitunglah keliling segitiga :
Jawab:
a. Luas segitiga Rumusnya yaitu ½ x a x t, sehingga
= 6 cm2
Jadi, hasil perhitungan dari luas segitiga adalah 6 cm2.
b. Keliling segitiga nya adalah = s + s + s, sehingga
= AC+AB+BC
= 3cm+4cm+5cm
= 12 cm.
Jadi, keliling segitiga adalah 12 cm.
4. Jajar genjang
Pengertian Bangun Datar Jajar genjang
Pengertian dari jajar genjang sendiri merupakan suatu bangun datar 2 dimensi yang dibentuk atas 2 buah pasang rusuk yang di mana pada masing – masing nya memiliki ukuran sama panjang serta sejajar dengan pasangan nya.
Kemudian jajar genjang memiliki 2 buah pasang sudut siku – siku yang di mana pada masing – masing sudutnya sama besar dengan sudut di depan nya.
Sifat Bangun Datar Jajar genjang
- Sifat pada Jajar Genjang tidak memiliki simetri lipat.
- Jajar Genjang memiliki simetri putar tingkat dua.
- Sudut Jajar Genjang yang berhadapan memiliki ukuran yang sama besar.
- Jajar Genjang memiliki 4 sisi serta 4 sisi sudut.
- Diagonal yang dimilikinya memiliki panjang yang tidak sama.
- Jajar Genjang memiliki 2 Pasang Sisi yang sejajar serta sama panjang.
- Jajar Genjang memiliki 2 buah sudut tumpul dan 2 buah sudut lancip.
Rumus yang ada pada Bangun Datar Jajar genjang
| Nama | Rumus |
| Keliling (Kll) | Kll = 2 × (a + b) |
| Luas (L) | L = a × t |
| Sisi Alas (a) | a = (Kll ÷ 2) – b |
| Sisi Sisi Miring (b) | a = (Kll ÷ 2) – a |
| t diketahui L | t = L ÷ a |
| a diketahui L | a = L ÷ t |
Contoh Soal
Perhatikanlah gambar jajaran genjang ABCD di bawah ini!
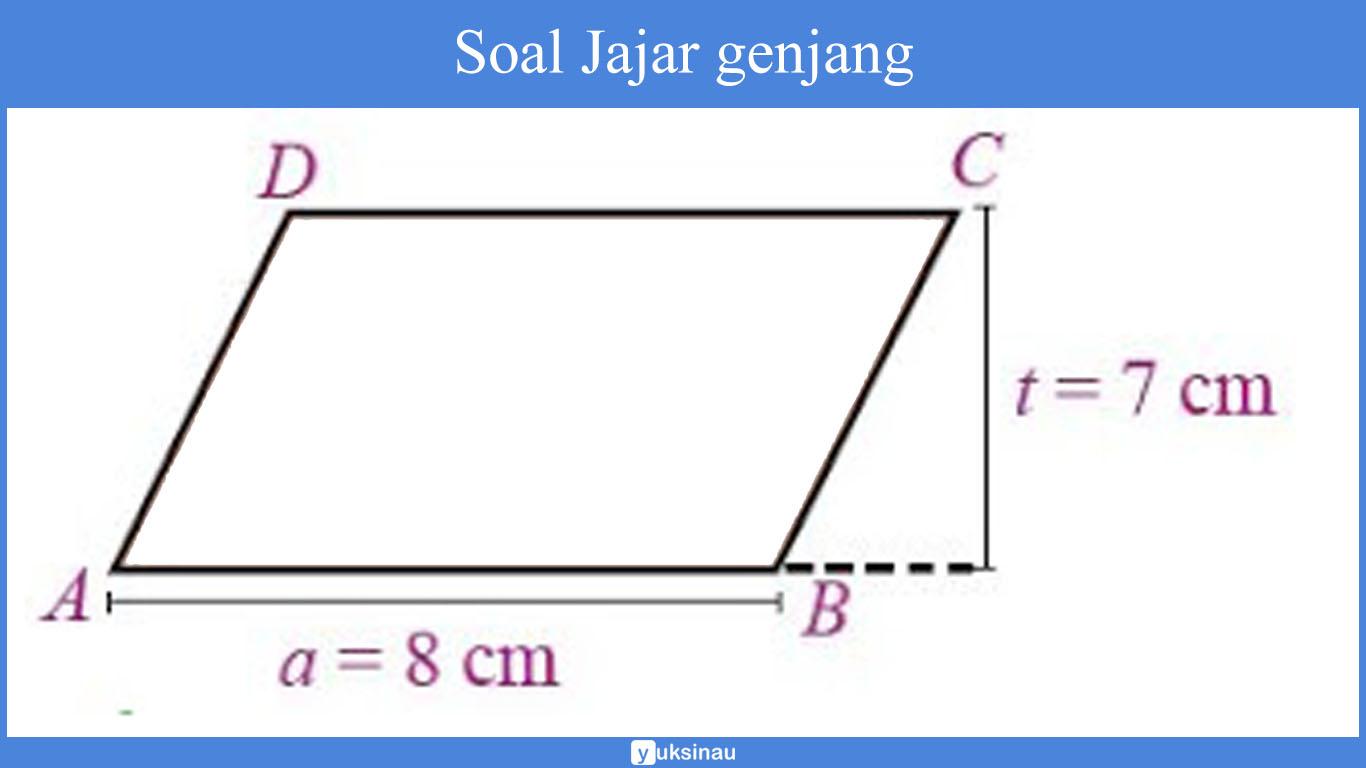
Panjang BC = DA = 8 cm.
Pertanyaan:
a. Hitunglah luas jajaran genjang ABCD, merupakan:
b. Hitunglah keliling jajaran genjang ABCD, merupakan:
Jawab:
a. Luas jajaran genjang ABCD adalah = a x t, sehingga
= 8 cm x 7 cm
= 56 cm2
Jadi, luas jajaran genjang ABCD yaitu 56 cm2.
b. Keliling jajaran genjang ABCD adalah s + s + s + s, maka:
K = AB + BC + CD + DA, yakni :
K = 8 cm + 8 cm + 8 cm + 8 cm
= 32 cm.
Jadi, keliling jajaran genjang ABCD adalah 32 cm.
5. Trapesium
Pengertian Bangun Datar Trapesium
Pengertian dari trapesium sendiri merupakan suatu bangun datar 2 dimensi yang dibentuk dari 4 buah rusuk yang 2 buah di antaranya merupakan saling sejajar namun panjang nya tidak sama.
Tetapi terdapat juga trapesium yang rusuk ketiganya merupakan tegak lurus pada rusuk – rusuk sejajar nya yang biasa dikenal dengan sebutan trapesium siku – siku.
Sifat Bangun Datar Trapesium
- Trapesium adalah bangun datar dengan 4 sisi (quadrilateral).
- Memiliki 2 sisi sejajar yang tidak sama panjang.
- Memiliki 4 buah titik sudut.
- Minimal pada bagun datar trapesium memiliki 1 titik sudut tumpul
- Trapesium memiliki 1 simetri putar.
Rumus yang ada pada Bangun Datar Trapesium
| Nama | Rumus |
| Luas (L) | 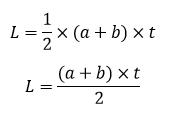 |
| Keliling (Kll) | Kll = AB + BC + CD + DA |
| Tinggi (t) | |
| Sisi a (CD) | 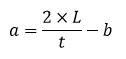 atau CD = Kll – AB – BC – AD atau CD = Kll – AB – BC – AD |
| Sisi b (AB) | 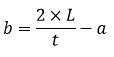 atau AB = Kll – CD – BC – AD atau AB = Kll – CD – BC – AD |
| Sisi AD | AD = Kll – CD – BC – AB |
| Sisi BC | BC = Kll – CD – AD – AB |
Contoh soal:
Perhatikanlah bangun datar trapesium EFGH di bawah ini!
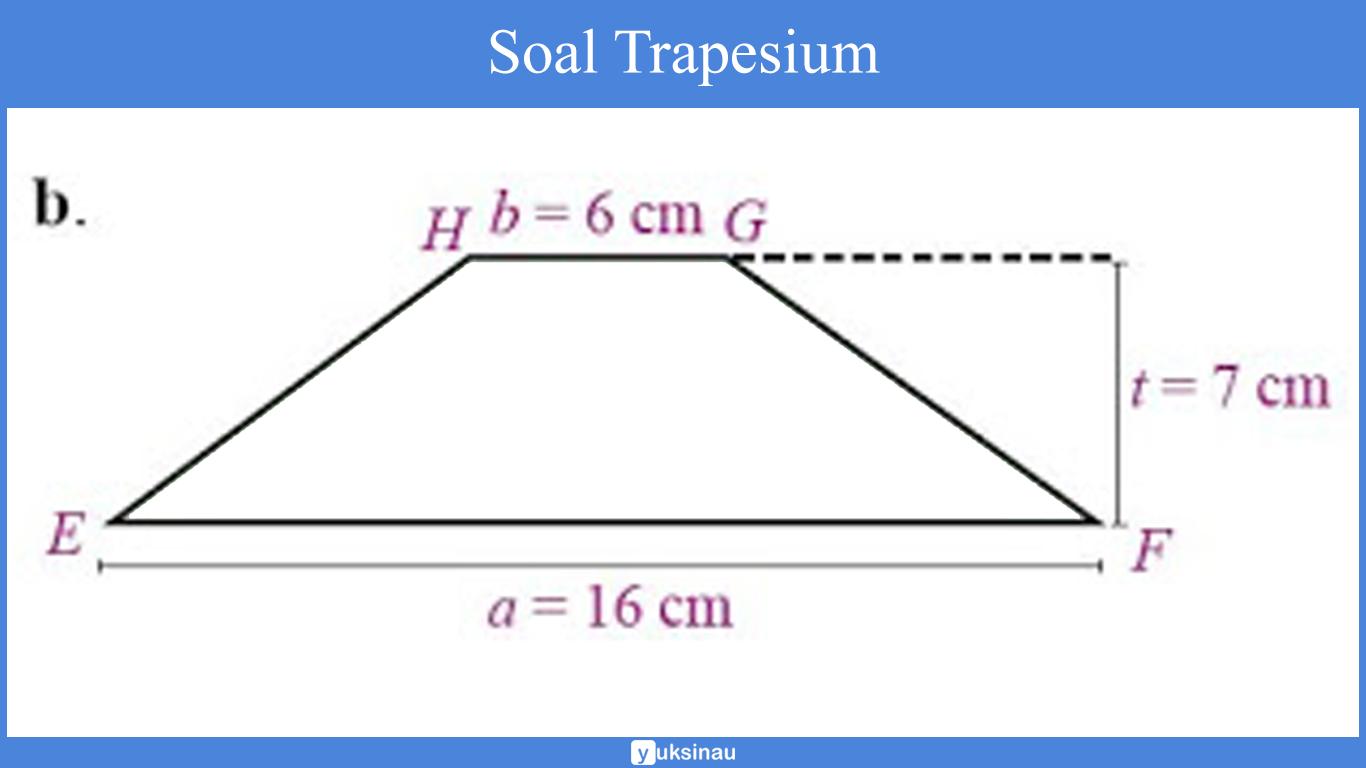
Panjang EH = FG ialah 8 cm.
Pertanyaan:
a. Tentukanlah luas trapesium EFGH:
b. Tentukanlah keliling trapesium EFGH:
Jawab:
a. Luas trapesium EFGH adalah: ½ x (a + b) x t maka,
= ½ x (16cm + 6 cm) x 7 cm
= ½ x 22 cm x 7 cm
= 11cm x 7 cm
= 77 cm2
Jadi, luas trapesium EFGH di atas adalah 77 cm2.
b. Keliling trapesium EFGH memiliki rumus yaknni: s + s + s + s, maka:
K = EF + FG + GH + HE
K = 16 cm + 8 cm + 6 cm + 8 cm
= 38 cm.
Jadi, luas keliling trapesium EFGH di atas adalah 38 cm.
6. Layang – layang
Pengertian dari layang – layang sendiri merupakan suatu bangun datar 2 dimensi yang di bentuk oleh 2 buah segitiga sama kaki serta berbentuk segiempat di mana memiliki alas yang berhimpitan dan berbentuk menjadi suatu layang – layang.
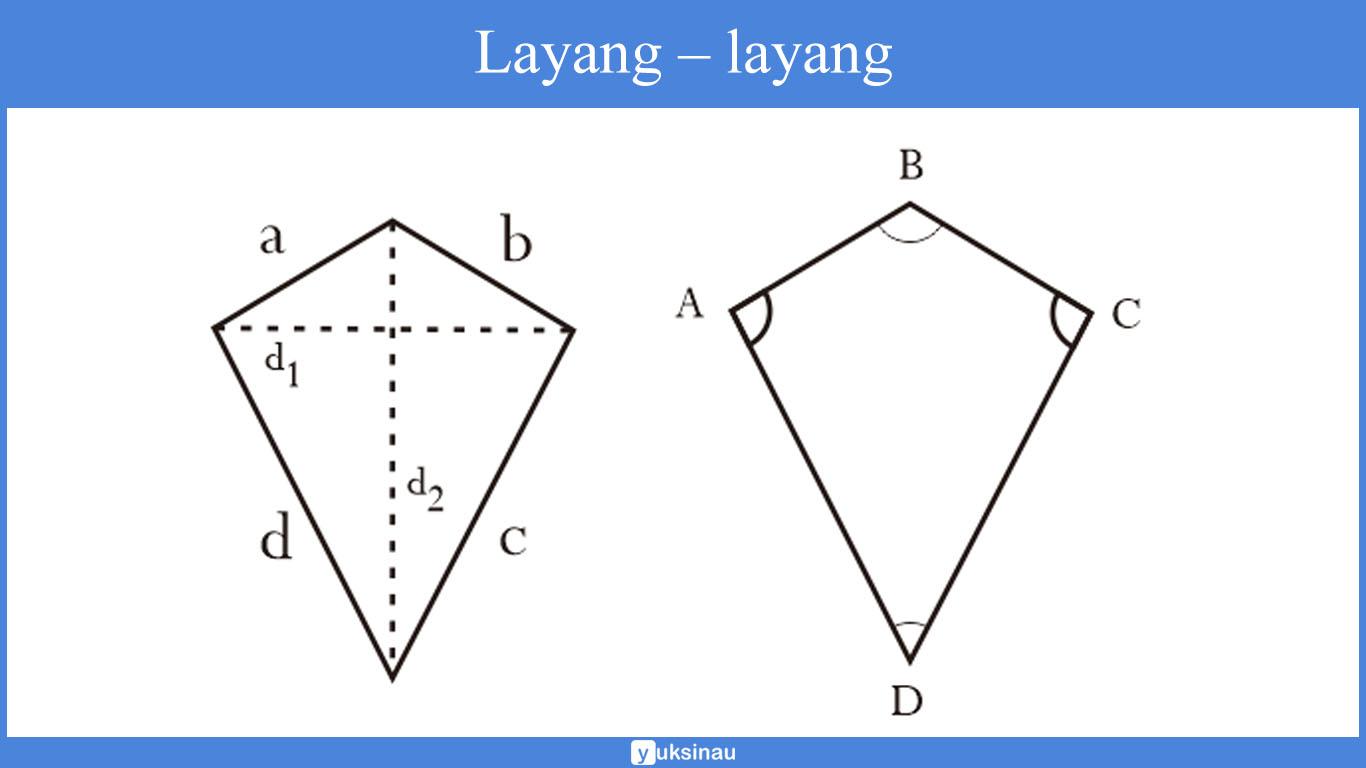
Sifat Bangun Datar Layang – layang
- Layang-layang adalah suatu bangun datar dengan 4 sisi (quadrilateral).
- Memiliki 2 pasangan sisi yang membentuk sudut yang berbeda.
Pasangan 1 merupakan sisi a dan b, membentuk sudut ∠ABC.
Pasangan 2 merupakan sisi c dan d, membentuk sudut ∠ADC. - Memiliki sepasang sudut yang saling berhadapan dengan besar ukuran yang sama.
Sudut ∠BAD serta ∠BCD saling berhadapan dan memiliki besar yang sama. - Memiliki 2 diagonal dengan panjang yang berbeda.
- Diagonal layang-layang saling tegak lurus (90º).
- Diagonal terpanjang adalah sumbu simetri layang-layang.
- Layang-layang hanya mempunyai 1 sumbu simetri.
Rumus yang ada pada Bangun Datar Layang – layang
| Nama | Rumus |
| Luas (L) | L = ½ × d1 × d2 |
| Keliling (Kll) | Kll = a + b + c + d |
| Kll = 2 × (a + c) | |
| Diagonal 1 (d1) | d1 = 2 × L ÷ d2 |
| Diagonal 2 (d2) | d2 = 2 × L ÷ d1 |
| a atau b | a = (½ × Kll) – c |
| c atau d | c = (½ × Kll) – a |
Contoh Soal
Perhatikan layang layang ABCD di bawah ini!
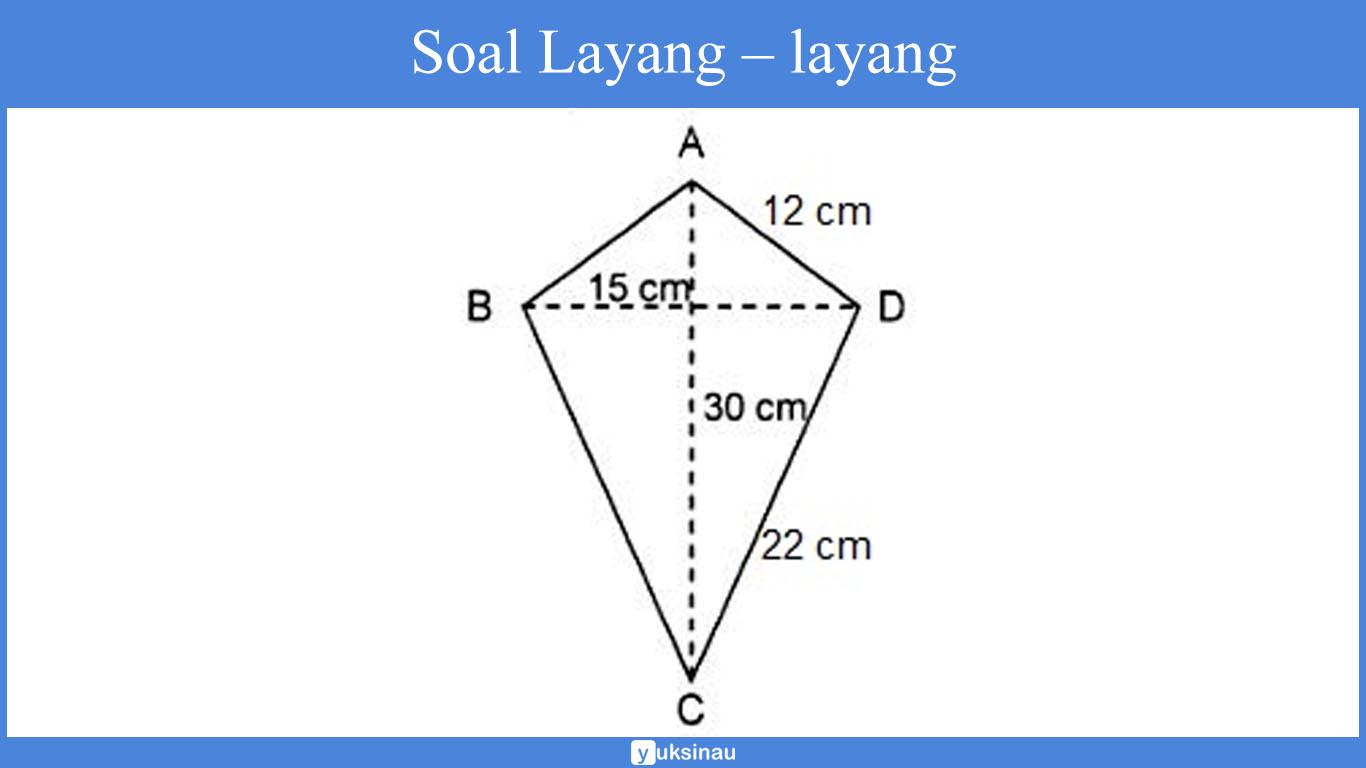
DiketahuI;
Panjang BC = panjang CD
Panjang AB = panjang AD
Pertanyaan:
a. Hitunglah luas layang layang ABCD!
b. Hitunglah keliling layang layang ABCD!
Jawab:
= ½ x AC x BD
= ½ x 30 cm x 15 cm
= 225 cm2
Jadi, luas layang layang ABCD tersebut yaitu 225 cm2.
b. Keliling dari layang-layang ABCD adalah: 2 x (x + y), sehingga
= 2 x (AB + BC)
= 2 x (12 cm + 22 cm)
= 2 x 34 cm
= 68 cm
Jadi, keliling layang layang ABCD yaitu 68 cm.
7. Belah Ketupat
Belah Ketupat merupakan suatu bangun datar 2 dimensi yang dibentuk oleh 4 buah sisi dengan ukuran sama panjang serta memiliki 2 pasang sudut bukan siku-siku dengan sudut yang saling berhadapan memiliki besar sama.
Dalam bahasa inggris, belah ketupat disebut sebagai rhombus.
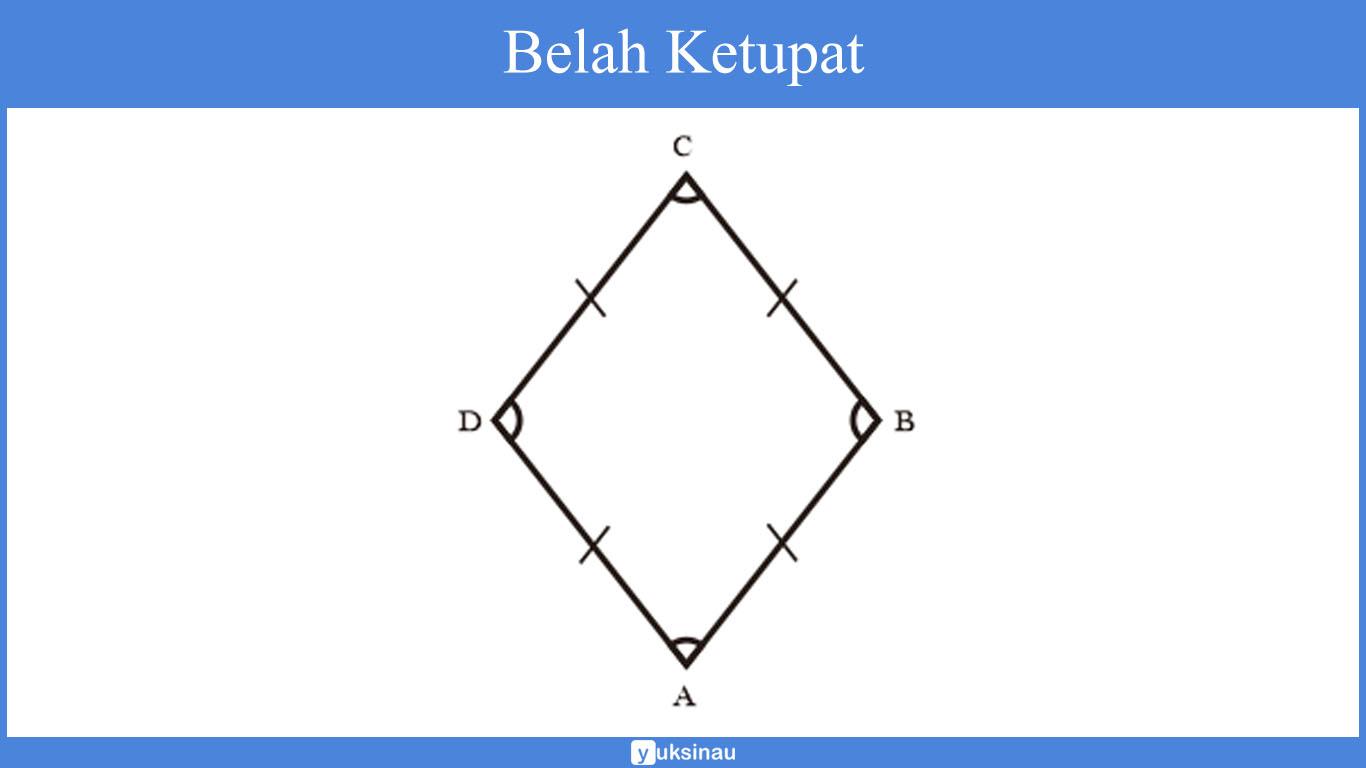
Sifat Bangun Datar Belah Ketupat
- Keempat sisinya sama panjang.
- Memiliki 2 diagonal yang saling tegak lurus.
Diagonal 1 (d1) dan diagonal 2 (d2) pada belah ketupat saling tegak lurus membentuk sudut siku-siku (90°). - Sudut yang saling berhadapan memiliki besar yang sama.
Pada belah ketupat sudut yang berhadapan memiliki besar yang sama. Ilustrasi di atas menunjukkan besar sudut ∠ABC = ∠ADC dan ∠BAD = ∠BCD. - Besar pada keempat titik sudutnya 360º.
- Memiliki 2 sumbu simetri yang di mana adalah diagonalnya.
- Belah Ketupat memiliki Simetri Putar tingkat 2.
- Memiliki 4 buah sisi dan 4 buah titik sudut.
- Keempat sisi belah ketupat mempunyai panjang yang sama.
Rumus yang ada pada Bangun Datar Belah Ketupat
| Nama | Rumus |
| Keliling (Kll) | Kll = s + s + s + s |
| Kll = s × 4 | |
| Luas (L) | L = ½ × d1 × d2 |
| Sisi (s) | s = Kll ÷ 4 |
| Diagonal 1 (d1) | d1 = 2 × L ÷ d2 |
| Diagonal 2 (d2) | d2 = 2 × L ÷ d1 |
Contoh Soal:
Perhatikan belah ketupat di bawah ini!
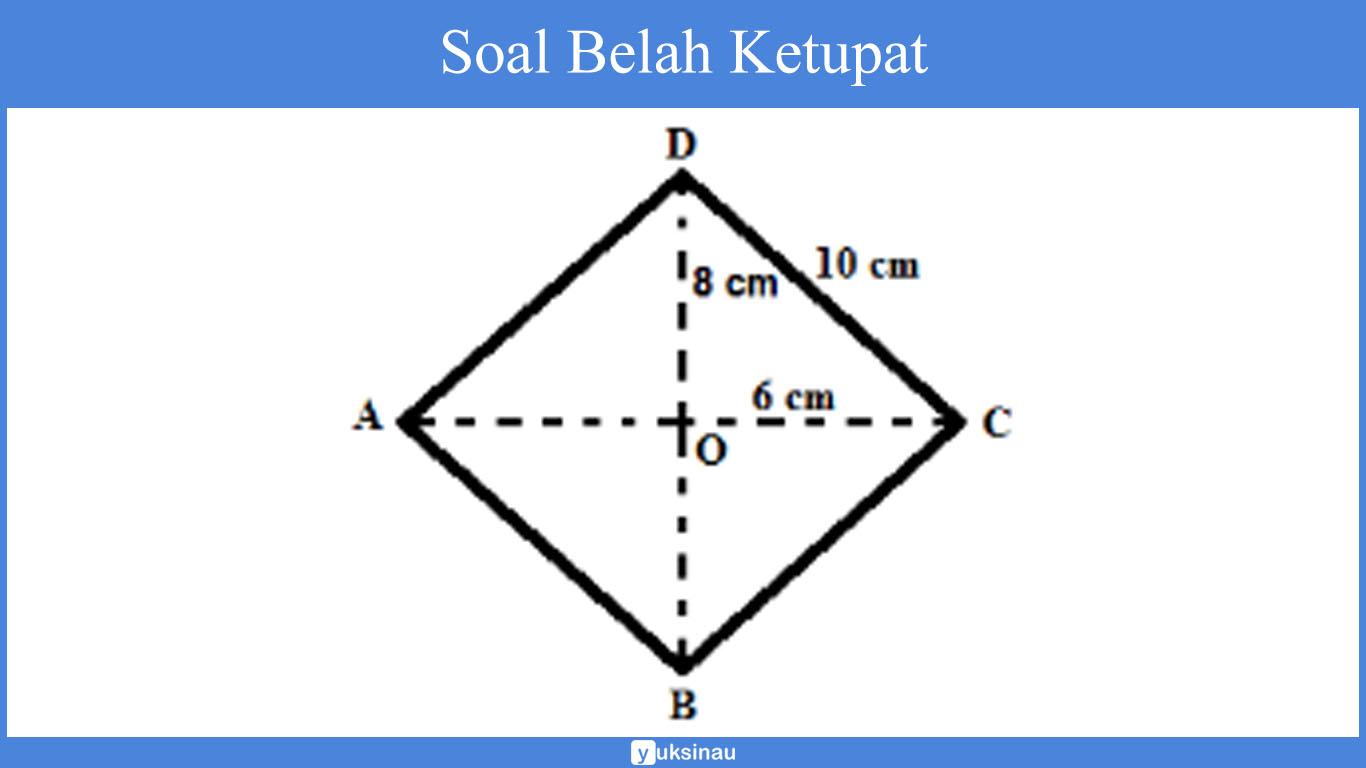
Panjang AC adalah 12 cm
Panjang BD adalah 16 cm
Pertanyaannya yaitu:
a. Tentukanlah luas belah ketupat ABCD!
b. Tentukan simak keliling belah ketupat ABCD!
Jawab:
a. Luas belah ketupat ABCD adalah = ½ x d1 x d2, sehingga
= ½ x AC x BD
= ½ x 12 cm x 16 cm
= 96 cm2
Jadi, luas belah ketupat ABCD yaitu 96 cm2.
b. Keliling belah ketupat ABCD adalah: s + s + s + s, sehingga
= AB + BC + CD + DA
= 4 x s
= 4 x 10 cm
= 40 cm
Jadi, keliling belah ketupat ABCD yaitu 40 cm.
8. Lingkaran
Pengertian Lingkaran
Lingkaran adalah bangun datar dua dimensi dibentuk oleh himpunan semua titik yang mempunyai jarak sama dari suatu titik tetap.
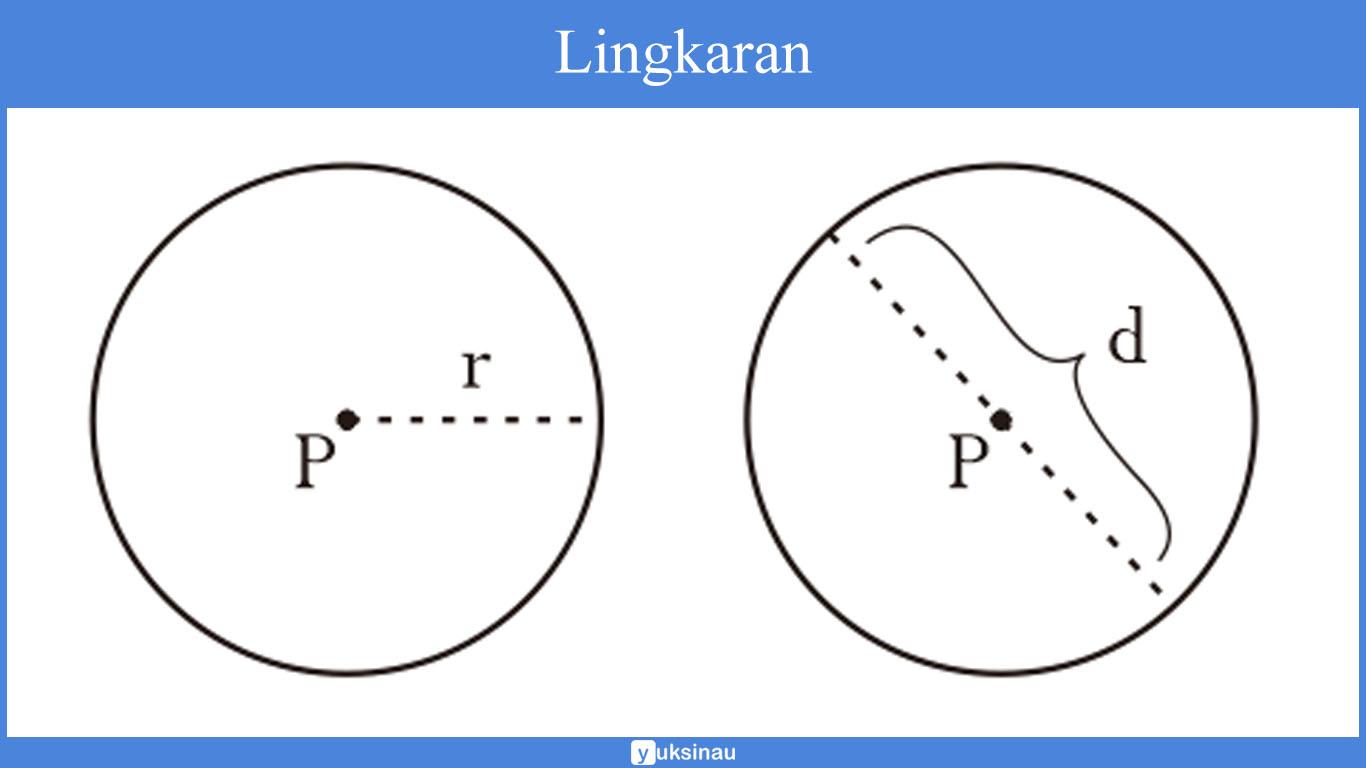
- Pusat lingkaran (P): Titik tetap pada lingkaran disebut sebagai pusat lingkaran.
- Jari-jari (r): jarak titik lainnya pada pusat lingkaran disebut sebagai jari-jari lingkaran.
- Garis lengkung: Himpunan seluruh titik lingkaran lalu membentuk garis lengkung yang menjadi keliling lingkaran.
- Diameter (d): garis yang ditarik oleh dari dua titik pada garis lengkung dan melewati titik pusat disebut sebagai diameter (d). Diameter lingkaran memiliki panjang 2 × r.
- phi (π): nilai perbandingan antara keliling serta diameter lingkaran selalu konstan yakni 3,14159 (dibulatkan menjadi 3,14) atau 22/7. Nilai ini didapatkan dari Keliling ÷ Diameter = phi.
Sifat Bangun Datar Lingkaran
- Mempunyai simetri putar tak terhingga.
- Mempunyai simetri lipat dan juga sumbunya yang tak terhingga.
- Tidak memiliki titik sudut.
- Memiliki satu buah sisi.
| Nama | Rumus |
| Diameter (d) | d = 2 × r |
| Jari-jari (r) | r = d ÷ 2 |
| Luas (L) | L = π x r x r atau L = π x r2 |
| Keliling (Kll) | Kll = π x d |
| Mencari r | r = kll/ 2π |
| r = √L/ √π |
Contoh Soal
Mencari Luas
Apabila diketahui suatu lingkaran memiliki diameter 14 cm. Berapakah luas lingkaran tersebut?
Jawab:
Diketahui:
- d = 14 cm
Sebab d = 2 × r maka:
r = d/2
r = 14/2
r = 7 cm
Ditanyakan:
- Luas lingkaran?
Penyelesaian:
Luas = π × r²
Luas = 22/7 × 7²
Luas = 154 cm²
Sehingga, luas lingkaran tersebut yaitu 154 cm².
Mencari Keliling
Hitunglah keliling lingkaran yang memiliki jari-jari 20 cm.
Jawab
Diketahui:
- r = 20 cm
- π = 3,14
Ditanyakan:
- Keliling lingkaran?
Jawab:
Keliling = 2 × π × r
Keliling = 2 × 3,14 × 20
Keliling = 125,6 cm
Sehingga, keliling lingkaran tersebut yaitu 125,6 cm.
Mencari Diameter
Diketahui suatu lingkaran mempunyai keliling sebesar 66 cm. Tentukan berapa diameter lingkaran tersebut!
Jawab
Diketahui:
- Keliling = 66 cm
Ditanyakan:
- Diameter lingkaran?
Jawab:
Keliling = π × d
Dalam mencari diameter, maka kita akan menggunakan rumus mencari diameter, yaitu:
Rumus mencari diamter ialah d = keliling / π
- d = 66 / (22/7)
- d = (66 × 7) / 22
- d = 21 cm
Sehingga, diameter lingkaran tersebut yaitu 21 cm.
Demikianlah ulasan singkat kali ini yang dapat kami sampaikan. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian.
The post Bangun Datar appeared first on Tuliskan.
ARTIKEL PILIHAN PEMBACA :
Comments
Post a Comment