Sistem Persamaan Linear Dua Variabel (SPLDV) - Poin 100
Keberadaan internet membuat siapa saja bisa mengakses berbagai informasi, maka tidak heran belakangan ini banyak sekali betebaran situs-situs yang membahas mengenai Sistem Persamaan Linear Dua Variabel (SPLDV). Hal ini sangat logis mengingat di era pandemi ini, masyarakat kita lebih sering melakukan proses belajar mengajar secara daring. Baiklah sudah cukup basa-basinya, yuk langsung masuk ke pembahasan saja.
Penjelasan Lengkap Sistem Persamaan Linear Dua Variabel (SPLDV)
Sistem Persamaan Linear Dua Variabel (SPLDV)- Persamaan linear dua variabel merupakan sebuah persamaan yang memuat dua variabel di mana pangkat atau derajat pada masing-masing variabelnya sama dengan satu.
Bentuk umum dari persamaan linear dua variabel yaitu:
ax + by = c
di mana x dan y merupakan variabel. Kemudian
Sistem Persamaan Linear Dua Variabel (SPLDV)
Sistem Persamaan Linear Dua Variabel atau yang biasa kita sebut sebagai SPLDV merupakan dua persamaan linear dua variabel yang mempunyai hubungan diantara keduanya serta mempunyai satu penyelesaian.
Bentuk umum dari sistem persamaan linear dua variabel yaitu:
ax + by = c
px + qy = d
Keterangan:
- x dan y disebut sebagai variabel
- a, b, p dan q disebut sebagai koefisien
- c dan r disebut sebagai konstanta
SPLDV pad aumumnya dimanfaatkan guna menyelesaikan masalah sehari-hari yang memerlukan pemakaian Matematika.
Sebagai contoh ketika hendak menentukan harga pada suatu barang, mencari keuntungan penjualan, hingga menentukan ukuran suatu benda..
Adapun beberapa langkah tertentu untuk menyelesaikan masalah dengan memakai SPLDV, antara lain:
- Mengganti setiap besaran yang terdapat dalam masalah tersebut dengan variabel (biasanya dilambangkan dengan huruf atau simbol).
- Membuat model Matematika dari masalah tersebut. Model Matematika ini kemudian dirumuskan dan mengikuti bentuk umum SPLDV.
- Mencari solusi dari model permasalahan tersebut dengan cara memakai metode penyelesaian SPLDV.
Suku, Koefisien, Konstanta dan Variabel
Suku merupakan suatu bagian dari bentuk aljabar yang bisa terdiri dari variabel dan koefisien atau dalam bentuk konstanta bahwa setiap suku dipisahkan oleh suatu tanda operasi suatu penjumlahan.
Sebagai contoh:
5x-y + 8,
Dalam kasus tersebut maka sukunya adalah 5x, -t dan 8
Variabel merupakan suatu pengganti dari suatu nilai atau angka yang pada umumnya ditunjukkan oleh huruf atau simbol.
Sebagai contoh:
Gilang mempunyai 6 ekor kambing dan juga 3 ekor sapi.
Jika kita tuliskan matematikan menjadi,
katakan: a = kambing dan b = sapi
Maka: 6a + 3b, dengan a dan b merupakan variabel
Koefisien merupakan sebuah angka yang menunjukkan jumlah variabel serupa.
Koefisien juga dapat disebut sebagai angka di depan variabel sebab menulis untuk suku yang memiliki variabel merupakan koefisien di depan variabel.
Sebagai contoh:
Setiawan mempunyai 7 ekor kambing dan uga 3 ekor sapi.
Jika kita tuliskan matematikanya menjadi,
katakan: a = kambing dan b = sapi
Maka: 7a + 3b, dengan 7 dan 3 koefisien
Dengan 7 koefisien a dan 3 merupakan koefisien b
Konstanta merupakan angka yang tidak diikuti oleh suatu variabel sehingga nilainya tetap (konstan) untuk nilai variabel apa pun.
Sebagai contoh:
5p + 3q – 10.
– 10 merupakan konstanta sebab apa pun nilai p dan q merupakan nilai -10 tidak terpengaruh, sehingga tetap (konstan).
Cara menyelesaikan Sistem Persamaan Linear Dua Variabel
1. Metode Eliminasi
Pada metode eliminasi digunakan guna menentukan himpunan penyelesaian dari sistem persamaan linear dua variabel.
Carangan yakni dengan cara menghilangkan atau mengeliminasi salah satu variabel dari sistem persamaan tersebut.
Jika variabel dinyatakan dengan x dan y, untuk menentukan variabel x maka kita harus mengeliminasi variabel y terlebih dahulu, begitu juga sebaliknya.
Coba perhatikan bahwa jika suatu koefisien dari salah satu variabel sama maka kita bisa mengeliminasi atau menghilangkan salah satu variabel tersebut.
Untuk lebih jelasnya, kami berikan contoh permasalahan di bawah ini:
Contoh:
Dengan metode eliminasi, tentukanlah himpunan penyelesaian sistem persamaan 2x + 3y = 6 dan x – y = 3 !
Penyelesaian:
2x + 3y = 6 dan x – y = 3
Langkah pertama yang harus kita lakukan adalah eliminasi variabel y.
Untuk mengeliminasi variabel y, maka koefisien y harus sama, sehingga persamaannya yakni: 2x + 3y = 6 dikalikan 1 dan persamaan
x – y = 3 dikalikan dengan 3.
2x + 3y = 6 × 1 2x + 3y = 6
x – y = 3 × 3 3x – 3y = 9
5x = 15
x = 15/5
x = 3
Langkah kedua yang harus kita lakukan adalah eliminasi variabel x.
Sama halnya pada langkah pertama, untuk mengeliminasi variabel x, maka koefisien pada x harus sama, sehingga persamaan yang kita dapat adalah 2x + 3y = 6 dikalikan 1 dan
x – y = 3 dikalikan 2.
2x + 3y = 6 ×1 2x + 3y = 6
x – y = 3 ×2 2x – 2y = 6
5y = 0
y = 0/5
y = 0
Sehingga, himpunan penyelesaiannya yaitu {(3,0)}.
2. Metode Substitusi
Metode Substitusi merupakan sebuah metode untuk menyelesaikan suatu sistem persamaan linear dua variabel dengan metode substitusi.
Yang mana kita akan menggunakan cara menyebutkan terlebih dahulu variabel yang satu ke dalam variabel yang lain dari suatu persamaan.
Kemudian menyubstitusikan (menggantikan) variabel tersebt ke dalam persamaan yang lainnya.
Contoh:
Dengan metode substitusi, tentukan himpunan penyelesaian dari persamaan berikut 2x +3y = 6 dan x – y = 3.
Penyelesaiannya:
Persamaan x – y = 3 merupakan ekuivalen dengan x = y + 3.
Dengan menyubstitusi persamaan x = y + 3 ke persamaan 2x + 3y = 6 maka bisa kita dapatkan data sebagai berikut:
2x + 3y = 6
ó 2 (y + 3) + 3y = 6
ó 2y + 6 + 3y = 6
ó 5y + 6 = 6
ó 5y + 6 – 6 = 6 – 6
ó 5y = 0
ó y = 0
Lalu untuk mendapatkan nilai x, maka substitusikan nilai y ke persamaan x = y + 3, sehingga akan kita peroleh:
x = y + 3
ó x = 0 + 3
ó x = 3
Sehingga, himpunan penyelesaiaanya yaitu {(3,0)}
3. Metode Gabungan
Metode gabungan merupakan sebuah cara untuk menyelesaikan sistem persamaan linear dua variabel dengan metode gabungan. Di mana kita akan menggabungkan metode eliminasi dan substitusi.
Contoh:
Dengan menggunakan metode gabungan di atas, tentukan himpunan penyelesaian dari sistem persamaan 2x – 5y = 2 dan x + 5y = 6 !
Penyelesaiannya:
Langkah pertama yang harus kita lakukan adalah dengan menerapkan metode eliminasi, sehingga akan kita peroleh:
2x – 5y = 2 ×1 2x – 5y = 2
x + 5y = 6 ×2 2x +10y = 12
-15y = -10
y = (-10)/(-15)
y = 2/3
Kemudian, disubstitusikan nilai y ke persamaan x + 5y = 6 sehingga akan kita peroleh:
x + 5y = 6
ó x + 5 (2/3) = 6
ó x + 10/15 = 6
ó x = 6 – 10/15
ó x = 22/3
Sehingga, himpunan penyelesaiaanya yaitu {(2 2/3,2/3)}
4. Metode Grafik
Penyelesaian SPLDV dengan menggunakan metode grafik dilakukan dengan cara menentukan koordinat titik potong dari kedua garis yang mewakili kedua persamaan linear.
Namun, sebelum menggunakan metode grafik ini, kalian perlu belajar bagaimana cara untuk menggambar garis pada persamaan linear terlebih dahulu.
- Menggambar garis yang mewakili kedua persamaan dalam bidang kartesius.
- Menentukan titik potong dari kedua grafik tersebut.
- Penyelesaiannya merupakan titik pada (x, y).
Permasalahan dalam SPLDV:
- Persamaan pertama: 2x + 3y = 8
- Persamaan Kedua: 3x + y = 5
Penyelesaian SPLDV dengan menggunakan metode grafik.
Langkah 1: menggambar kedua grafik
Menentukan titik potong pada kedua sumbu x dan y dari kedua persamaan tersebut.

Reperesentasi kedua persamaan dalam bidang kartesius.
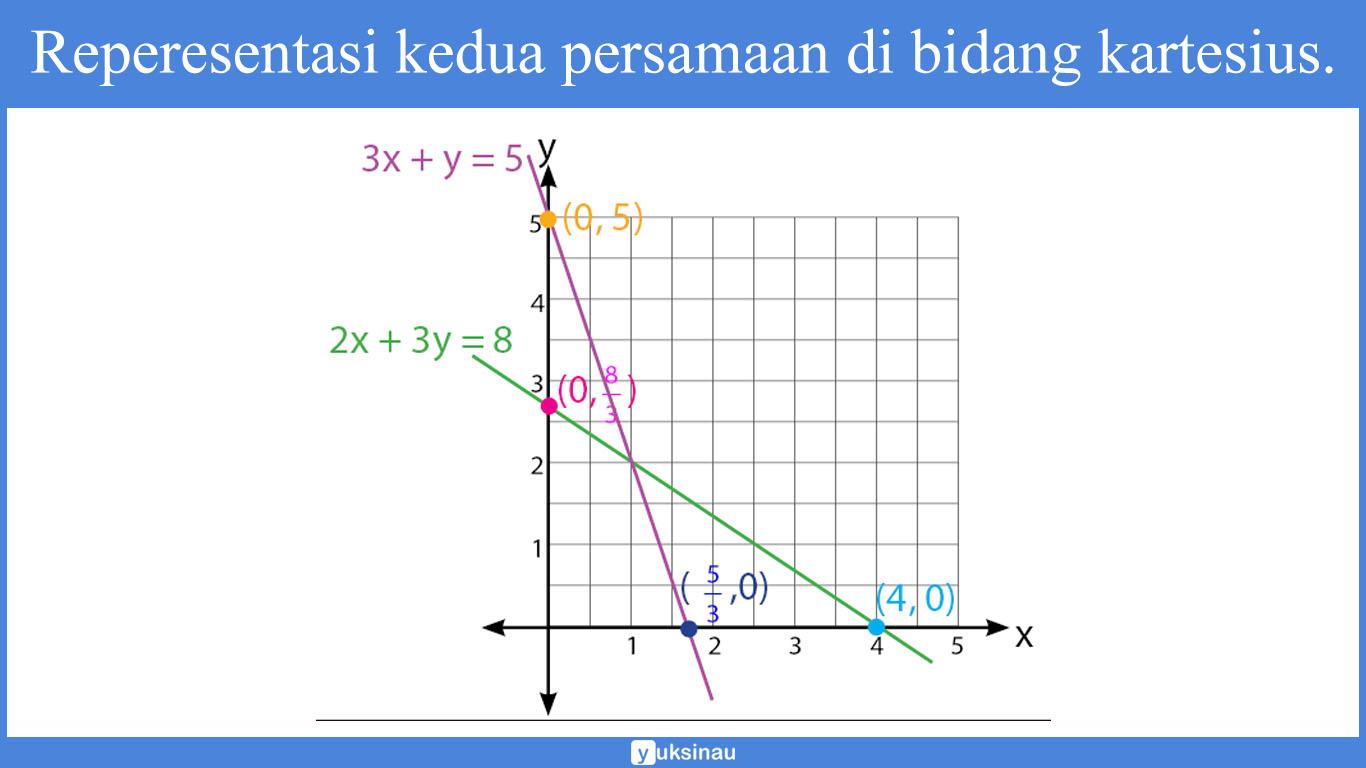
Langkah 2: menemukan titik potong dari kedua grafik tersebut.

Langkah 3: peyelesaiannya adalah (x, y)
Berdasarkan gambar bisa kita ketahui bahwa titik potongnya berada pada x = 1 dan y = 2
Maka daerah penyelesaiannya yaitu (1, 2)
Contoh Soal
Beriktu akan kami berikan beberapa contoh soal cerita dan juga soal yang pernah ada di UN. Berikut ulasan selengkapnya.
Soal 1.
Putra ingin melakukan lompat tali. Misalnya, tali yang dipakai oleh Putra mempunyai panjang 70 cm lebih pendek dari tinggi Putra.
Supaya tali tidak tersangkut di tubuh Putra, maka setidaknya tali yang digunakan harus mempunya panjang dua kali lebih panjang dari ukuran sebelumnya.
Sehingga, jika diukur kembali, maka ukuran dua kali panjang tali akan 30 cm lebih panjang dari tinggi Putra.
Tentukan berapa ukuran panjang tali yang digunakan serta tinggi badan Putra! Serta tentukan berapa panjang tali yang digunakan supaya tidak tersangkut di badan Putra!
Jawab:
- Langkah pertama yang bisa kita lakukan yaitu dengan cara mengganti seluruh besaran yang terdapat di dalam soal dengan variabel. Disini kita misalkan seperti:
x = panjang tali (dalam cm) dan y = tinggi badan (dalam cm)
- Membuat model Matematika dari permasalahan soal.
Panjang tali 70 cm lebih pendek dari tinggi Kumamon → x = y – 70 atau -x + y = 70
Dua kali panjang tali 30 cm lebih panjang dari tinggi Kumamon → 2x = 30 + y atau 2x – y = 30
Sehingga, model Matematika dari soal di atas yaitu:
- Persamaan I : -x + y = 70
- Persamaan II : 2x – y = 30
Sampai disini kalian paham kan? Nah, setelah ini kita akan menentukan nilai dari x dan y dengan menggunakan empat metode penyelesaian SPLDV. Simak baik-baik ya.
1. Metode grafik
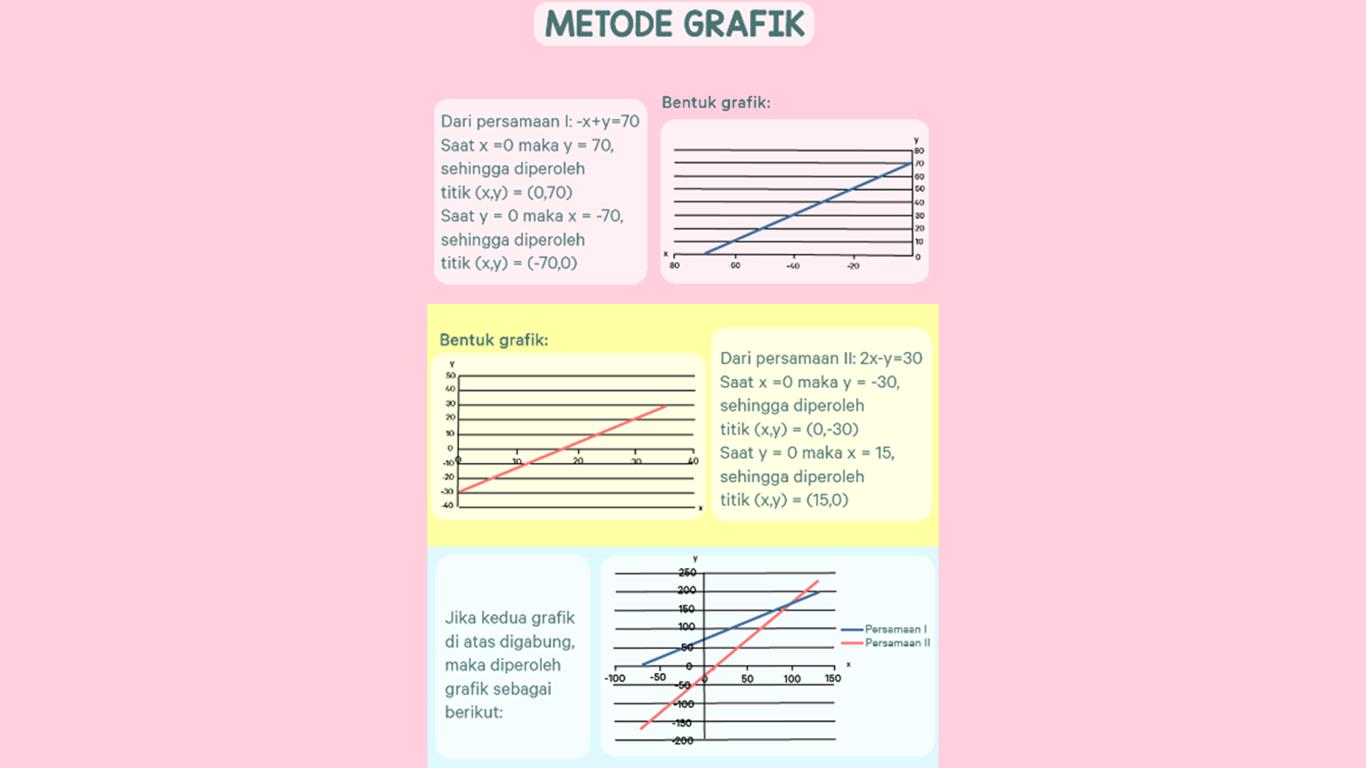
Sehingga, akan kita dapatkan titik potong dari kedua garis yaitu (x,y) = (100,170).
Sebelumnya, kita sudah mengibaratkan panjang tali dengan variabel x dan tinggi Putra dengan variabel y.
Maka, sudah bisa ditentukan nih berapa panjang tali dan juga tinggi si Putra itu. Yups! Jawabannya yaitu 100 cm untuk panjang tali serta 170 cm untuk tinggi Putra.
Gampang kan? Metode grafik ini biasanya berguna apabila nilai koefisien dan nilai konstanta dari persamaannya bukan merupakan bilangan bulat, sehingga akan lebih baik jika digambar untuk memudahkan mencari nilai dari x dan y nya.
2. Metode eliminasi
Diketahui:
- Persamaan I : -x + y = 70
- Persamaan II : 2x – y = 30
Untuk mencari nila x, samakan koefisien y
-x + y = 70
2x – y = 30
Sebab koefisien y dari kedua persamaan tersebut sudah sama, maka bisa langsung kita selesaikan dengan menggunakan operasi penjumlahan untuk menghilangkan nilai y.
-x + y = 70
2x – y = 30
________ +
x =100
Untuk mencari nilai y, samakan koefisien x
-x + y = 70 |x2|
2x – y = 30 |x1|
Suapya koefisien x dari kedua persamaan sama, maka kalikan persamaan I dengan 2 dan kalikan persamaan II dengan 1.
Kemudian, selesaikan dengan menggunakan operasi penjumlahan untuk menghilangkan nilai x.
-2x + 2y = 140
2x – y = 30
_________ +
y = 170
3. Metode substitusi
Diketahui:
- Persamaan I : -x + y = 70
- Persamaan II : 2x – y = 30
Untuk mencari nilai x, maka cari nila y terlebih dahulu.
Daro persamaan I: -x + y = 70 → y = 70 + x
Kemudian, subsitusi nilai y ke dalam persamaan II:
2x – y = 30
→ 2x-(70+x) = 30
→ 2x-70-x = 30
→ x-70 = 30
→ x= 100
Setelah itu, subsitusikan nilai x ke persamaan y = 70 + x
y = 70 + x
→ y = 70 + 100
→ y= 170
Berdasarkan metode substitusi, kita peroleh nilai x = 100 dan y = 170. Sehingga, bisa kita ketahu jika tinggi badan Putra adalah sebesar 170 cm serta tali yang digunakan oleh Putra untuk bermain lompat tali sepanjang 100 cm.
4. Metode gabungan
Diketahui:
- Persamaan I : -x + y = 70
- Persamaan II : 2x – y = 30
Misalkan, kita akan mencari nilai x terlebih dahulu dengan menggunakan metode eliminasi. Maka untuk menentukan nilai x samakan koefisien y.
-x + y = 70
2x – y = 30
Karena koesifisien y dari kedua persamaan sudah ada, maka dapat langsung diselesaikan dengan menggunakan operasi penjumlahan untuk menghilangkan nilai y.
x + y = 70
2x – y = 30
________ +
x =100
Setelah diperoleh nilai x, subsitusikan nilai x ke salah satu persamaan untuk memperoleh nilai y.
Misalnya, dilakukan subtitusi nilai x ke dalam persamaan I, maka:
-x + y = 70
→ 100 + y = 70
→ y = 70 + 100
→ y = 170
Berdasarkan dari metode gabungan, didapatkan nilai x = 100 dan y = 170. Sehingga, bisa kita ketahui jika panjang tali sepanjang 100 cm serta tinggi Putara adalah 170 cm.
Perlu kalian ketahui jika metode gabungan ini adalah metode yang paling banyak digunkan untuk menyelesaikan masalah SPLDV.
Kemudian, kita akan mencari tahu berapa panjang tali yang dibutuhkan supaya Putra bisa bermain lompat tali tanpa harus tersangkut di tubuhnya.
Apabila kalian baca kembali contoh soal di atas, maka bisa kita ketahui jika setidaknya, tali tersebut harus dua kali lebih panjang dari ukuran sebelumnya (2x).
Sehingga, sudah bisa kita ketahui ya kalau panjang tali yang dibutuhkan supaya tidak tersangkut di tubuh Putra yaitu 2x = 2(100) = 200 cm.
Walaupun kelihatannya panjang dan rumit, namun apabila kalian memperbanyak latihan soal, pasti akan mudah, kok. Semangat terus ya.
Soal 1 (UN 2016)
Seorang tukang parkir mendapat uang sebesar Rp17.000,00 dari 3 buah mobil dan 5 buah motor, sedangkan dari 4 buah mobil dan 2 buah motor ia mendapat uang Rp18.000,00. Jika terdapat 20 mobil dan 30 motor, banyak uang parkir yang diperoleh adalah….
A. Rp135.000,00
B. Rp115.000,00
C. Rp110.000,00
D. Rp100.000,00
Jawab:
Misalkan:
Mobil = x dan motor = y
Ditanyakan: 20x + 30y = ….?
Model matematika:
3x + 5y = 17.000 ……(1)
4x + 2y = 18.000 ……(2)
Eliminasi persamaan (1) dan (2) akan didapatkan:
3x + 5y =17.000 | x4 |12x + 20y = 68.000
4x + 2y =18.000 | x3 |12x + 6y = 54.000 –
⟺ 14y = 14.000
⟺ y = 14.000/14
⟺ y = 1.000
Subtitusi nilai y = 1.000 ke salah satu persamaan:
3x+ 5y = 17.000
⟺ 3x + 5(1.000) = 17.000
⟺ 3x + 5.000 = 17.000
⟺ 3x = 17.000 – 5.000
⟺ 3x = 12.000
⟺ x = 12.000/3
⟺ x = 4.000
Maka, biaya parkir 1 mobil Rp4.000,00 dan 1 motor Rp1.000,00
20x + 30y = 20(4.000) + 30(1.000)
= 80.000 + 30.000
= 110.000
Sehingga, banyak uang parkir yang didapatkan sebesar Rp110.000,00
(Jawaban: C)
Soal 2 (UN 2015)
Di dalam kandang terdapat kambing dan ayam sebanyak 13 ekor. Jika jumlah kaki hewan tersebut 32 2kor, maka jumlah kambing dan ayam masing-masing adalah….
A. 3 dan 10
B. 4 dan 9
C. 5 dan 8
D. 10 dan 3
Jawab:
Misalkan:
Kambing = x dan ayam = y
Jumlah kaki kambing = 4 dan kaki ayam = 2
Ditanyakan: Jumlah kambing dan ayam = …?
Model matematika:
x + y = 13 ……(1)
4x + 2y = 32 ……(2)
Eliminasi persamaan (1) dan (2) akan kita dapatkan:
x + y = 13 | x4 | 4x + 4y = 52
4x + 2y = 32 | x1 | 4x + 2y = 32 –
⟺ 2y = 20
⟺ y = 20/2
⟺ y = 10
Subtitusi nilai y = 10 ke salah satu persamaan:
x + y = 13
⟺ x + 10 = 13
⟺ x = 13 – 10
⟺ x = 3
Sehingga, jumlah kambing = 3 ekor dan ayam = 10 ekor.
(Jawaban : A)
Demikianlah ulasan singkat terkait Sistem Persamaan Linear Dua Variabel (SPLDV) yang dapat kami sampaikan. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian.
The post Sistem Persamaan Linear Dua Variabel (SPLDV) appeared first on Yuksinau.
ARTIKEL PILIHAN PEMBACA :
Comments
Post a Comment