Relasi dan Fungsi - Poin 100

Relasi dan Fungsi - Selamat pagi, siang, sore, atau pun malam untuk Anda para pembaca situs Poin 100. Bagaimana hari kalian? Semoga selalu di liputi kebahagiaan. Nah di hari yang menyenangkan ini, kami akan mengulas tentang "Relasi dan Fungsi" yang mungkin saja sedang Anda cari beberapa waktu lalu.

Keberadaan internet membuat siapa saja bisa mengakses berbagai informasi, maka tidak heran belakangan ini banyak sekali betebaran situs-situs yang membahas mengenai Relasi dan Fungsi. Hal ini sangat logis mengingat di era pandemi ini, masyarakat kita lebih sering melakukan proses belajar mengajar secara daring. Baiklah sudah cukup basa-basinya, yuk langsung masuk ke pembahasan saja.

Penjelasan Lengkap Relasi dan Fungsi

Relasi dan Fungsi- Materi relasi dan fungsi merupakan salah satu dasar kita guna memasuki ke materi yang lainnya seperti limit fungsi, turunan, dan yang lainnya.

Sehingga, kalian perlu memperhatian dengan baik ulasan yang nanti akan diberikan dibawah ini ya. Oke, langsung aja ke materi intinya.

Relasi dan Fungsi

Mula-mula kita akan membahas mengenai relasi terlebih dahulu. Relasi merupakan sebuah aturan yang memasangkan anggota himpunan satu ke himpunan yang lain.

Sebuah relasi yang terdapat dalam himpunan A dengan himpunan B biasa disebut sebagai pemasangan atau korespondensi dari anggota yang terdapat di dalam himpunan A ke anggota yang terdapat di dalam himpunan B.

Sebagai contoh: suatu himpunan A = {0, 1, 2, 5}; B = {1, 2, 3, 4, 6}, maka relasi dari himpunan A dengan himpunan B dapat di sajikan ke dalam diagram panah, diagram cartesius, himpunan pasangan berurutan, serta rumusnya dapat kita lihat pada gambar di bawah ini.

a. Diagram panah

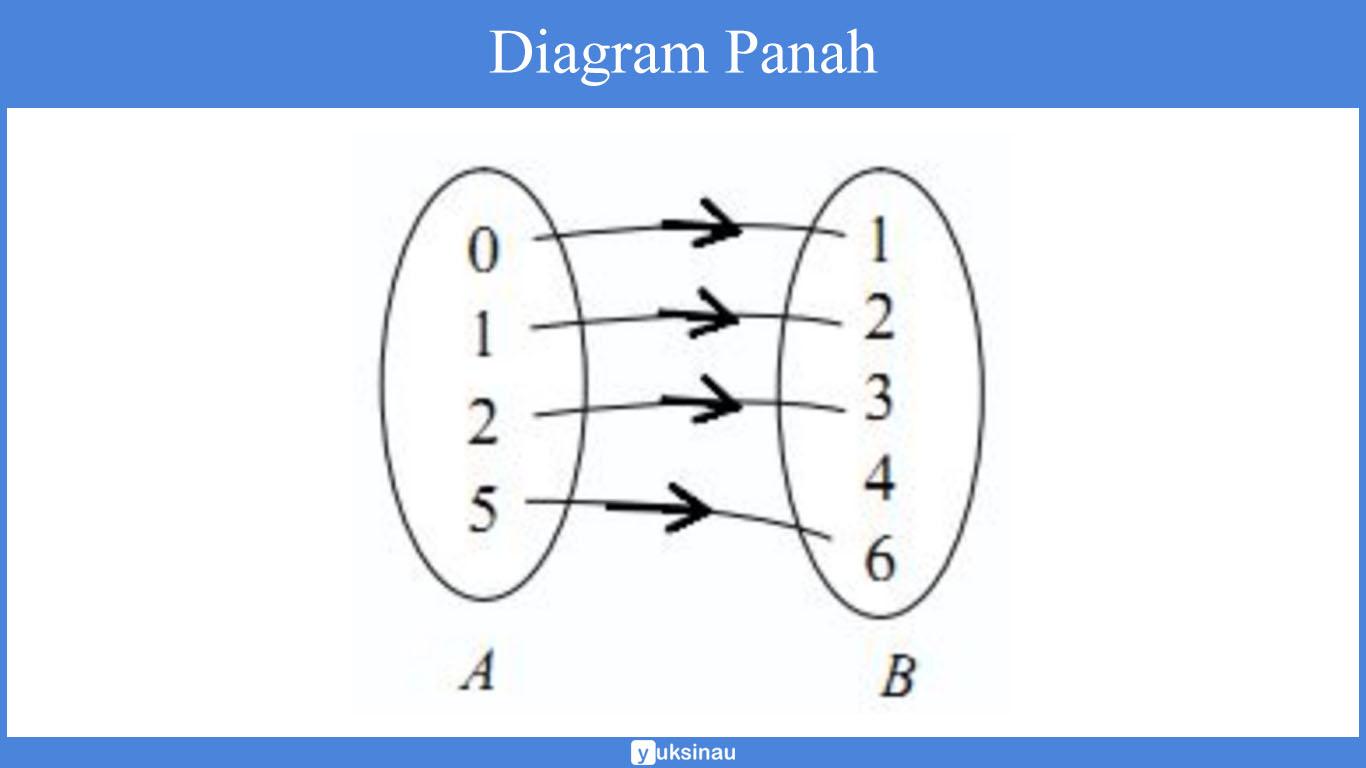
b. Diagram cartesius

c. Himpunan pasangan berurutan

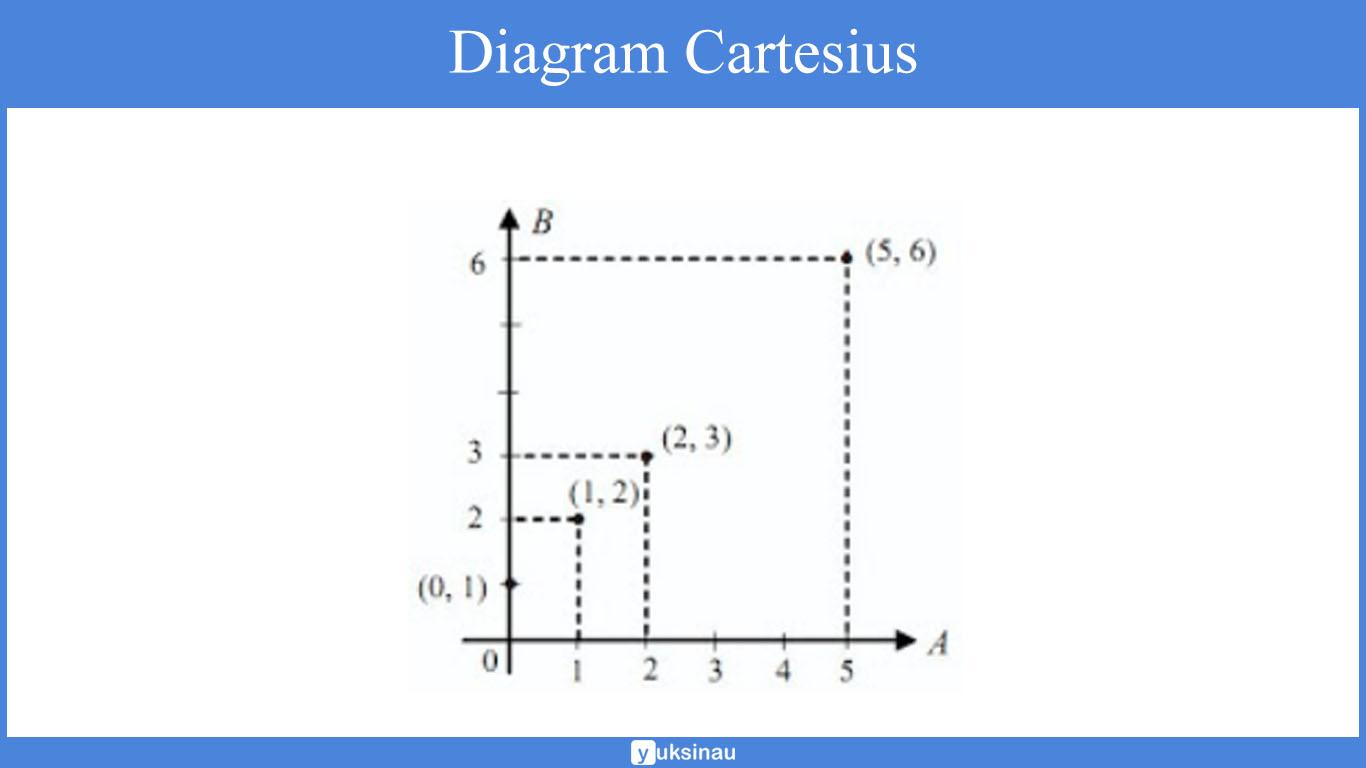
R = {(0, 1), (1, 2), (2, 3), (5, 6)}

d. Rumus

f(x) = x + 1, dimana x ∊ {0, 1, 2, 5} dan f(x) ∊ {1, 2, 3, 4, 6}

Pengertian Fungsi

Apabila sebelumnya pada bagian relasi dari himpunan A dan himpunan B dalam fungsi disebut sebagai fungsi dari A ke B apabia setiap anggota A dipasangkan dengan tepat satu anggota B.

Maka pada fungsi anggota dari himpunan A disebut sebagai domain (daerah asal). Sementara anggota dari himpunan B disebut sebagai kodomain (daerah kawan). Serta anggota yang ada dalam himpunan B yang berpasangan (himpunan C) disebut sebagai range (hasil) dari fungsi f.

Contoh soal 1.

Diketahui A = {1, 2, 3, 4} serta B = {1, 2, 3, 4, 5, 6, 7, 8}. Sebuah fungsi f: A → B ditentukan oleh f(x) = 2x – 1. Maka:

a. Gambarlah fungsi f dengan menggunakan diagram panah.

b. Tentukan range dari fungsi f.

c. Gambarlah grafik dari fungsi f

Jawab:

a.

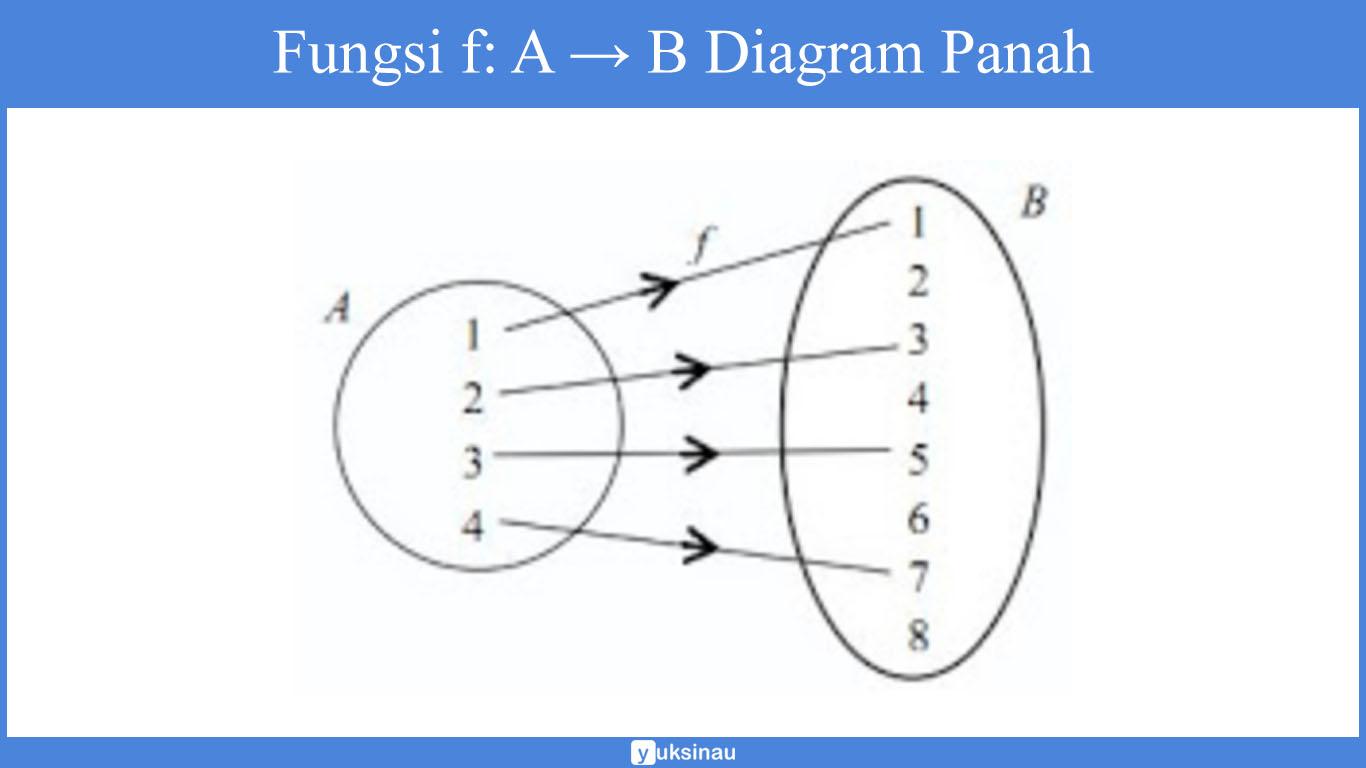
b. f(x) = 2x – 1

f(1) = 2.1 – 1 = 1                         f(3) = 2.3 – 1 = 5

f(2) = 2.2 – 1 = 3                         f(4) = 2.4 – 1 = 7

Sehingga, range dari fungsi f yaitu {1, 3, 5, 7}

c. Grafik fungsi

Macam-Macam Fungsi

1. Fungsi konstan (fungsi tetap)

Sebuah fungsi f: A → B ditentukan dengan rumus f(x) disebut sebagai fungsi konstan jika dalam setiap anggota domain fungsi selalu berlaku f(x) = C.

Yang mana C adalah bilangan yang konstan. Untuk lebih jelasnya dapat kalian lihat contoh di bawah ini.

Contoh soal 2.

Diketahui f: R → R dengan rumus f(x) = 3 dengan daerah domain {x | -3 ≤ x < 2}. Maka tentukanlah gambar grafiknya dari fungsi di atas!

Jawab:

2. Fungsi linier

Fungsi linier adalah fungsi f(x) = ax + b, yang mana a ≠ 0, a dan b termasuk ke dalam bilangan konstan. Grafik linier berbentuk garis lurus. Untuk lebih jelasnya dapat kalian lihat contoh di bawah ini.

Contoh soal 3.

Apabila diketahui f(x) = 2x + 3, maka tentukanlah gambar grafiknya.

Jawab:

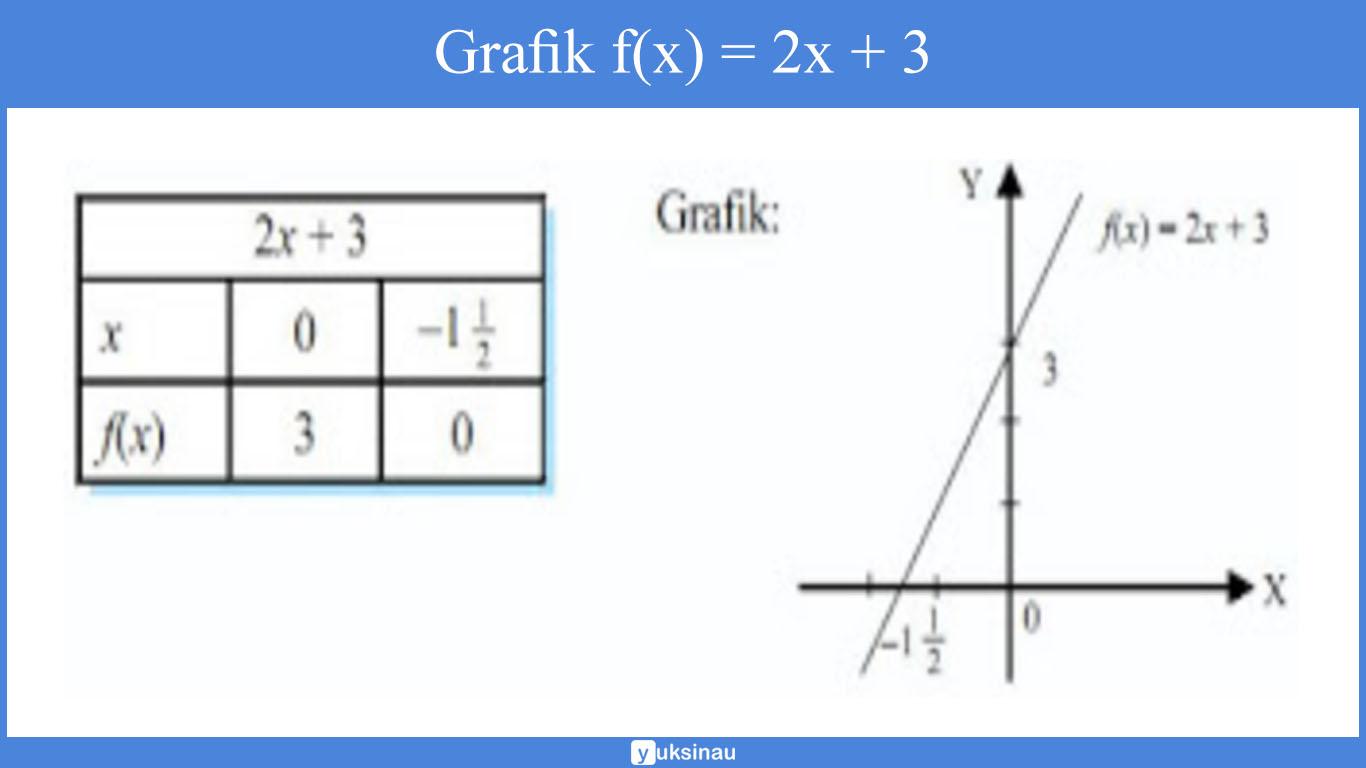
3. Fungsi kuadrat

Fungsi kuadrat adalah fungsi f(x) = ax² + bx + c, yang mana a ≠ 0 dan a, b, dan c merupakan bilangan konstan. Grafik kuadrat berbentuk seperti parabola. Untuk lebih jelasnya dapat kalian lihat contoh di bawah ini.

Contoh soal 4.

Perhatikan gambar di bawah ini, fungsi f ditentukan oleh f(x) = x² + 2x – 3

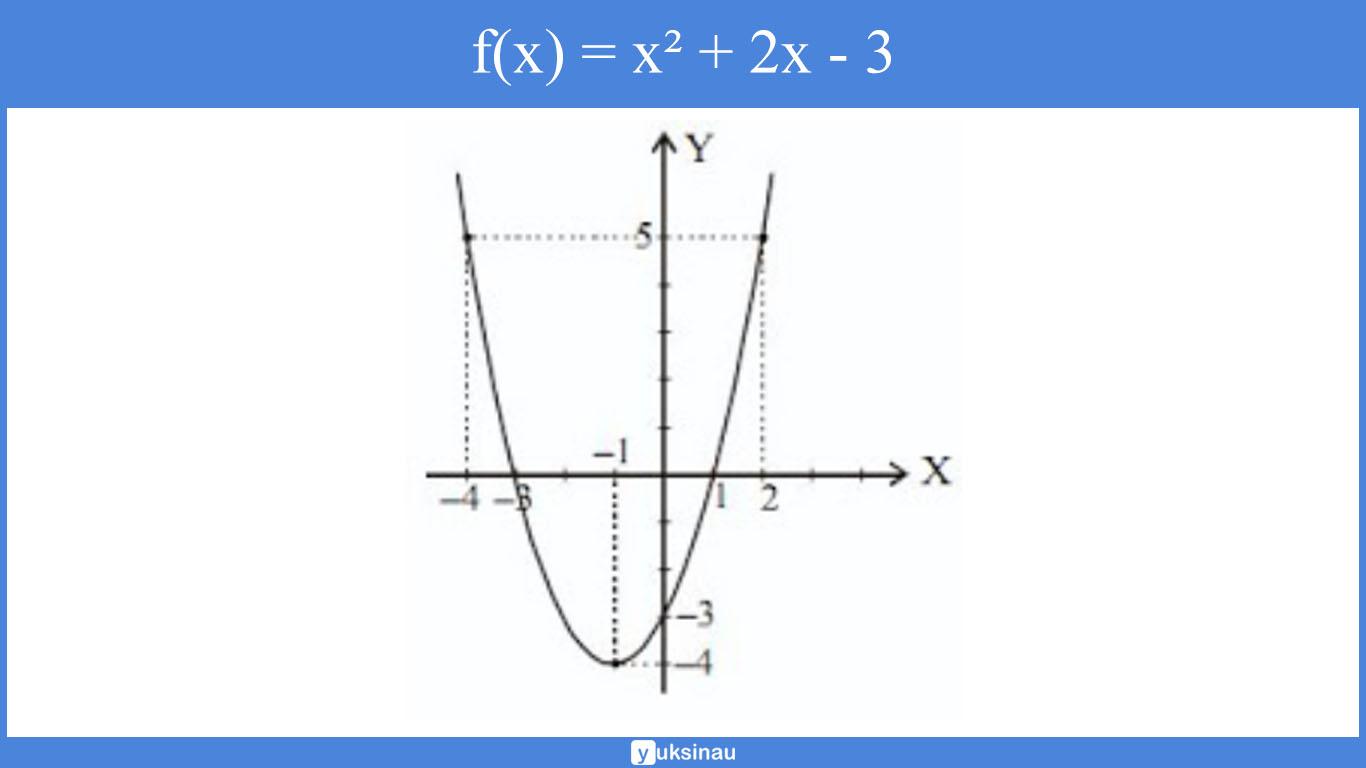
Maka tentukan:

1. Domain fungsi f
2. Nilai minimum fungsi f.
3. Nilai maksimum fungsi f.
4. Range fungsi f adalah adalah {y | -4 ≤ x < 5}
5. Pembuat nol fungsi f.
6. Koordinat titik balik minimum.

Jawab:

1. Domain fungsi f yaitu {x | -4 ≤ x < 2}.
2. Nilai minimum fungsi f yaitu -4.
3. Nilai maksimum fungsi f yaitu 5
4. Range fungsi f yaitu {y | -4 ≤ x < 5}
5. Koordinat titik balik minimum grafik fungsi f yaitu (-1, -4)

4. Fungsi identitas

Fungsi identitas adalah fungsi di mana berlaku f(x) = x atau setiap anggota domain dan atau daerah asal dari fungsi dipetakan pada dirinya sendiri.

Grafik fungsi identitas adalah berupa garis lurus yang melalui titik asal serta seluruh titik melalui ordinat yang sama.

Fungsi identitas akan ditentukan oleh f(x) = x. Untuk lebih jelasnya dapat kalian lihat contoh di bawah ini.

Contoh soal 5.

Fungsi f(x) = x untuk setiap x.

a. Tentukan nilai dari f(-2), f(0), f(1), f(3)

b. Gambarlah grafiknya.

Jawab:

a. f(x) = x

   f(-2) = -2

   f(0) = 0

   f(1) = 1

   f(3) = 3

b. Grafik

5. Fungsi tangga (bertingkat)

Fungsi tangga adalah fungsi f(x) yang berbentuk interval sejajar. Untuk lebih jelasnya dapat kalian lihat contoh di bawah ini.

Contoh soal 6.

Diketahui fungsi f(x) = -1, apabila x < 1
= 0, apabila -1 < x < 2
= 2, apabila 2 < x < 4

                                   = 3, apabila x > 4Tentukanlah inteval yang terbentuk dari:

a. f(-2)

b. f(0)

c. f(3)

d. f(3)

e. gambarlah grafik yang terbentuk dari data di atas.

Jawab:

a. f(-2) = -1

b. f(0) = 0

c. f(3) = 2

d. f(3) = 3

e.

6. Fungsi modulus (mutlak)

Fungsi modulus (mutlak) merupakan fungsi yang memetakan setiap bilangan real dakan daerah asal suatu fungsi menjadi nilai mutlak.

7. Fungsi ganjil dan fungsi genap

Sebuah fungsi f(x) disebut sebagai fungsi ganjil apabila berlaku f(-x) = –f(x) serta disebut sebagai fungsi genap dan apabila berlaku f(-x) = f(x).

Apabila fungsi f(-x) ≠ –f(x) dan f(-x) ≠ f(x) maka bukan termasuk fungsi ganjil dan juga fungsi genap. Untuk lebih jelasnya dapat kalian lihat contoh di bawah ini.

Contoh soal 7.

Tentukan fungsi f di bawah ini termasuk fungsi ganjil, fungsi genap, atau tidak.

a. f(x) = 2x³ + x

b. f(x) = 3 cos x – 5

c. f(x) = x² – 8x

Jawab:

a. f(x) = 2x³ + x

    f(-x) = 2(-x)³ + (-x)

            = -2x³ – x

            = -(2x³ + x)

            = -f(x)

    Sehingga, fungsi f(x) di atas merupakan fungsi ganjil.

b. f(x) = 3 cos x³ – 5

    f(-x) = 3 cos (-x) – 5

            = 3 cos x – 5

            = f(x)

    Sehingga, fungsi f(x) di atas merupakan fungsi genap.

c. f(x) = x² – 8x

    f(-x) = (-x)² – 8(-x)

            = x² + 8x

   Fungsi f(-x) ≠ –f(x) dan f(-x) ≠ f(x)

Sehingga, fungsi f(x) di atas bukan merupakan fungsi ganjil dan fungsi genap

Contoh Soal UN Relasi dan Fungsi

Soal 1.

Rumus suatu fungsi dinyatakan dengan f(x) = 2x + 5. Jika f(a) = 7, nilai a adalah ….     (UN 2009)

a. -1                                                            c. 2

b. 1                                                             d. 3

Jawab:

Rumus sebuah fungsi dinyatakan dengan f(x) = 2x + 5

f(a) = 7

maka

2a + 5 = 7

⇔  2a  = 7 – 5

⇔  2a  = 2

⇔    a  = 1

Sehingga nilai a yaitu 1.    (jawaban b)

Soal 2.

Diketahui rumus fungsi f(x) = -1-x. Nilai f(-2) adalah …  (UN 2010)

a. 3                                                            c. -1

b. 1                                                             d. -3

Jawab:

f(x) = -1-x

f(-2) = -1-(-2)

f(-2) = -1+2

f(-2) = 1

(jawaban b)

Soal 3.

Diketahui fungsi f(x) = 4x²+2x+5. Nilai f(½) = …

a. 6                                                           c. 8

b. 7                                                           d. 10

Jawab:

f(x) = 4x²+2x+5

f(½) = 4(½)²+2(½)+5

f(½) = 4(1/4) + 1 + 5

f(½) = 1 + 6

f(½) = 7

(jawaban b)

Soal 4.

Suatu fungsi ditentukan dengan rumus f(x) = px + q. Jika f(-2) = 17 dan f(5) = -32, maka f(12) = …

a. -81                                                      c. 29

b. -43                                                      d. 87

Jawab:

f(x) = px + q

f(-2) = 17 → -2p + q = 17

f(5) = -32 →  5p + q = -32
__________________-

-7p  = 49

p  = 49/-7

p  = -7

Substitusikan p = -7 ke salah satu persamaan, kita daoat memilih persamaan mana saja. Disini akan kita ambil -2p + q = 17, sehingga akan diperoleh:

-2p + q = 17

⇔ -2(-7) + q = 17

⇔       14 + q = 17

⇔               q  = 17 – 14

⇔                q  = 3

Maka,

f(x) = px + q

f(x) = -7x + 3

f(12) = -7(12) + 3

f(12) = -84 + 3

f(12) = -81

(jawaban a)

Baca juga: Sistem Persamaan Linear Tiga Variabel (SPLTV)

Demikianlah ulasan singkat terkait Relasi dan Fungsi yang dapat kami sampaikan. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian.

The post Relasi dan Fungsi appeared first on Yuksinau.

ARTIKEL PILIHAN PEMBACA :

Memuat...

Ketika Anda membaca kalimat ini, berarti Anda sudah sampai dibagian akhir dari pembahasan tentang Relasi dan Fungsi - Poin 100. Besar harapan kami ulasan yang kami sampaikan diatas bisa menjadi sarana pembelajaran untuk kita semua, terutama untuk Anda yang memang sedang mencarinya. Tak lupa kami sampaikan banyak terima kasih karena sudah berkunjung ke situs poin100. blogspot. com dan membaca hingga selesai. Salam santun dan sampai ketemu di artikel selanjutnya.