Segiempat - Poin 100

Segiempat - Selamat pagi, siang, sore, atau pun malam untuk Anda para pembaca situs Poin 100. Bagaimana hari kalian? Semoga selalu di liputi kebahagiaan. Nah di hari yang menyenangkan ini, kami akan mengulas tentang "Segiempat" yang mungkin saja sedang Anda cari beberapa waktu lalu.

Keberadaan internet membuat siapa saja bisa mengakses berbagai informasi, maka tidak heran belakangan ini banyak sekali betebaran situs-situs yang membahas mengenai Segiempat. Hal ini sangat logis mengingat di era pandemi ini, masyarakat kita lebih sering melakukan proses belajar mengajar secara daring. Baiklah sudah cukup basa-basinya, yuk langsung masuk ke pembahasan saja.

Penjelasan Lengkap Segiempat

Pernahkah kalian memperhatikan bentuk lapangan futsal? Lapangan futsal pada umumnya berbentuk segiempat. Di mana segiempat ini merupakan suatu bangun datar yang mempunyai 4 sisi dan 4 sudut.

Secara umum segiempat terbagi menjadi beberapa jenis, antara lain persegi, persegi panjang, jajargenjang, belah ketupat, layang-layang dan trapesium.

Tak hanya itu saja, ada juga sebuah bangun datar yang termasuk dalam bangun segiempat tetapi mempunyai bentuk tidak beraturan.

Supaya kalian dapat lebih mengenal mengenai segiempat dan juga jenis-jenisnya, yuk simak pembahasan di bawah ini!

Jenis Jenis Segiempat

Dalam artikel kali ini, kalian akan belajar mengenai jenis atau macam darii sifat bagun segiempat sekaligus rumusnya.

Terdapat beberapa jenis bangun yang masuk ke dalam bangun datar segiempat. Antara lain: persegi, persegi panjang, jajargenjang, trapesium, belah ketupat, serta layang-layang.

Berikut penjelasannya pada masing-msaing bangun.

A. Persegi

Persegi adalah suatu bangun segiempat yang memiliki panjang sisi yang sama besar. Sebagai contoh adalah papan catur.

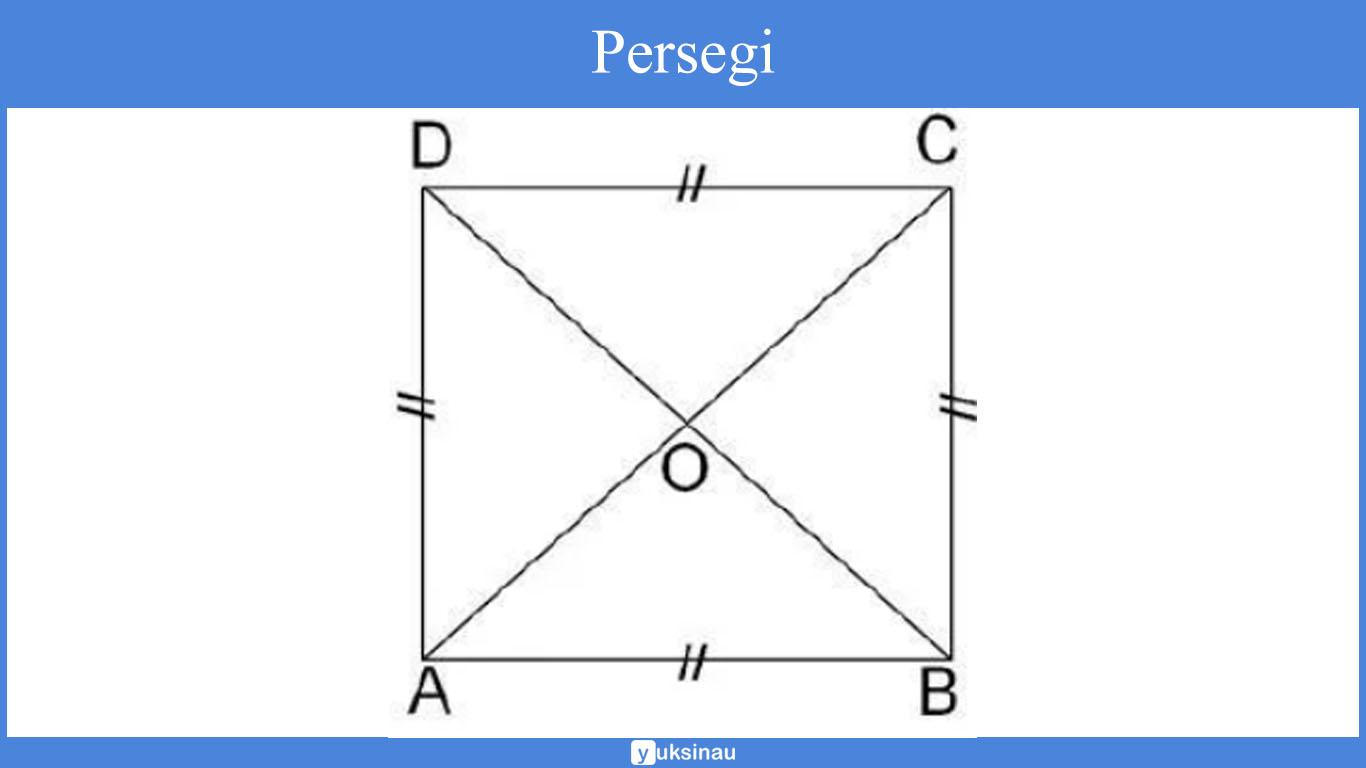
Sifat persegi:

1. Mempunyai 4 buah sumbu simetri serta simetri putar tingkat 4.
2. Bisa menempati bingkainya dengan 8 cara.
3. Keempat sisinya memiliki sama panjang (AB = BC = CD = AD).
4. Sisi-sisi yang berhadapan sejajar (AB // CD dan BC // AD)
5. Pada masing-masing sudutnya sama besar (∠A = ∠B = ∠C = ∠D =90°) .
6. Diagonal-diagonalnya sama panjang (BD = AC).
7. Diagonal-diagonalnya saling berpotongan tegak lurus serta membagi dua sama panjang (AO = OC = BO = OD).

Rumus Persegi:

• Sisi-sisi: s
• Luas: L = s x s = s²
• Keliling: K = 4 x s

Baca juga: Rumus Segitiga

B. Persegi Panjang

Persegi panjang adalah suatu bangun segi empat yang keempat sudutnya siku-siku serta sisi-sisi yang berhadapan sama panjang dan sejajar. Sebagai contoh yaitu lapangan sepak bola.

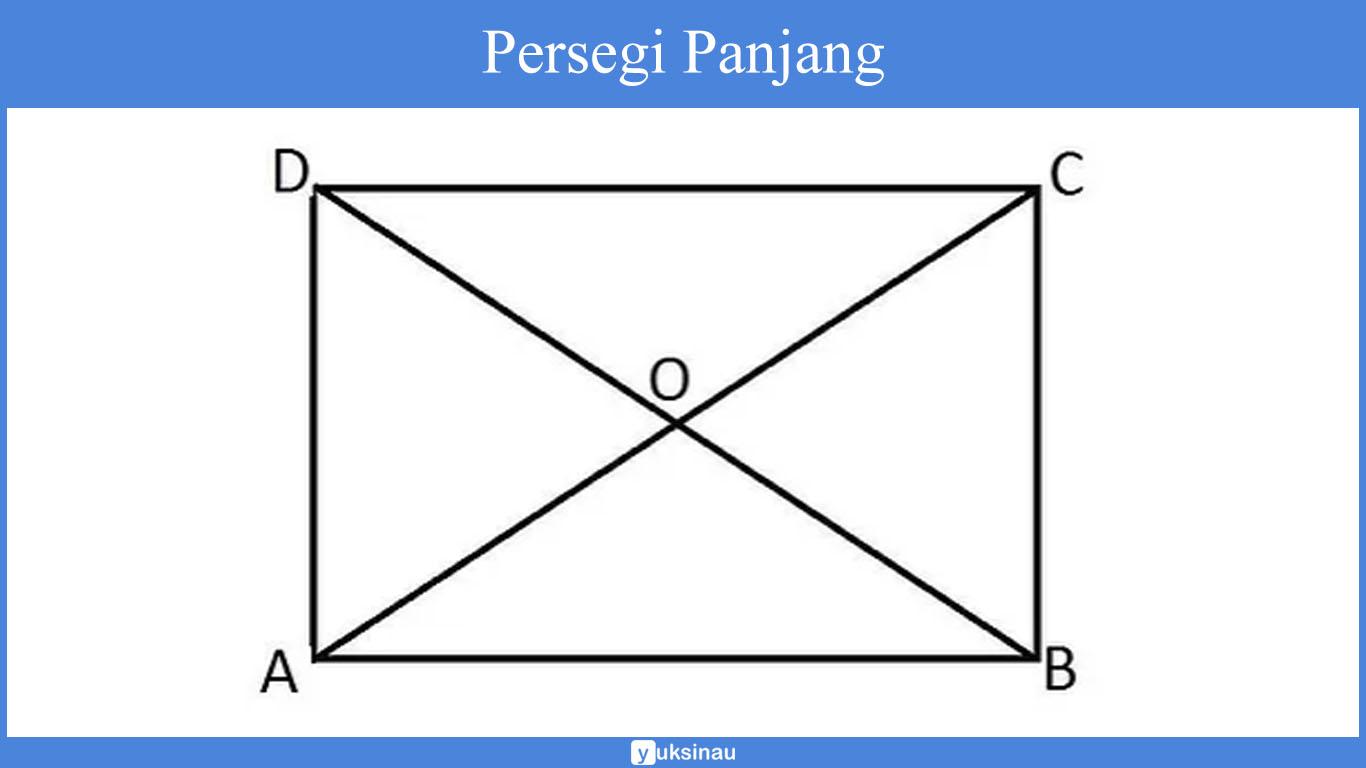
Sifat persegi panjanng:

1. Mempunyai 2 buah sumbu simetri serta simetri putar tingkat 2.
2. Bisa menempati bingkainya dengan 4 cara.
3. Sisi-sisi yang berhadapan sama panjang (AB = DC dan AD = BC).
4. Sisi-sisi yang berhadapan sejajar (AB // DC dan AD // BC).
5. Pada masing-masing sudutnya sama besar (∠A = ∠B = ∠C = ∠D =90°) .
6. Diagonal-diagonalnya sama panjang (AC = BD).
7. Diagonal-diagonal saling berpotongan serta membagi dua sama panjang (AO = OC = BO = OD).

Rumus persegi panjang:

• P: panjang
• L: lebar
• Luas: L = p x l
• Keliling: K = p + l + p + l atau K = 2 x (p + l)

C. Jajar Genjang

Jajar genjang merupakan bangun segi empat di mana masing-masing pasang sisinya berhadapan sama panjang dan juga sejajar. Sebagai contoh yaitu makanan wajik.

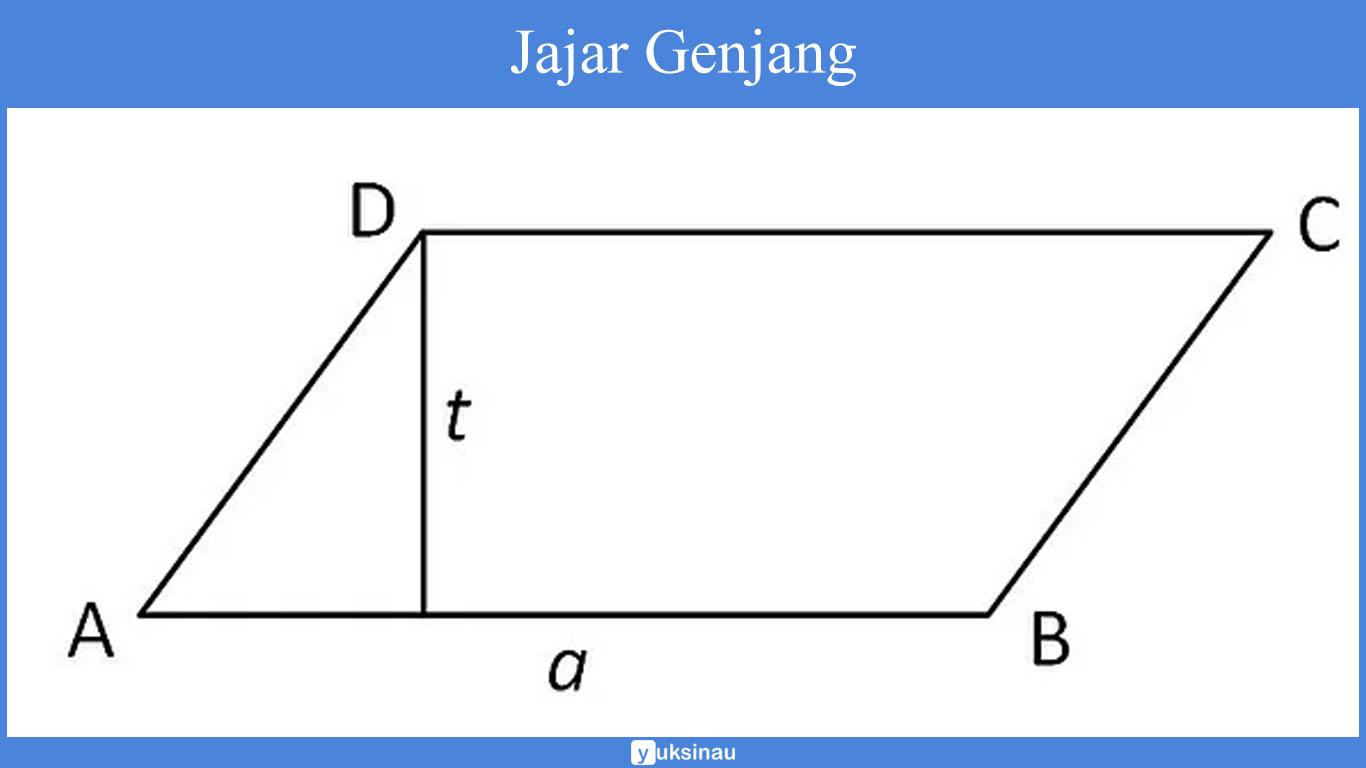
Sifat jajar genjang:

1. Sisi yang berhadapan sejajar serta sama panjang (AB = DC dan AB // DC, AD = BC dan AD // BC)
2. Sudut-sudut yang berhadapan sama besarnya yaitu  ∠A = ∠C dan ∠B = ∠D.
3. Dua sudut yang berdekatan berjumlah 180^o atau saling berpelurus yaitu: ∠A + ∠B = ∠B + ∠C  = ∠C + ∠D = ∠D + ∠A = 180°.
4. Jumlah semua sudutnya = 360^o
5. Diagonal-diagonalnya membagi jajargenjang menjadi dua bagian sama besar.
6. Kedua diagonal berpotongan di tengah-tengah (titik P) serta saling membagi dua sama panjang (AP = PC dan BP = PD).

Rumus jajar genjang:

• Alas: a
• Tinggi: t
  alas dan tinggi haruslah tegak lurus
• Luas: L = a x t
• Keliling: K = AB + BC + CD + DA = Jumlah semua sisi

D. Trapesium

Trapesium merupakan bangun segi empat yang mempunyai tepat sepasang sisi sejajar. Trapesium di bagi menjadi 2 macam, yakni Trapesium Sama Kaki serta Trapesium Siku-Siku.

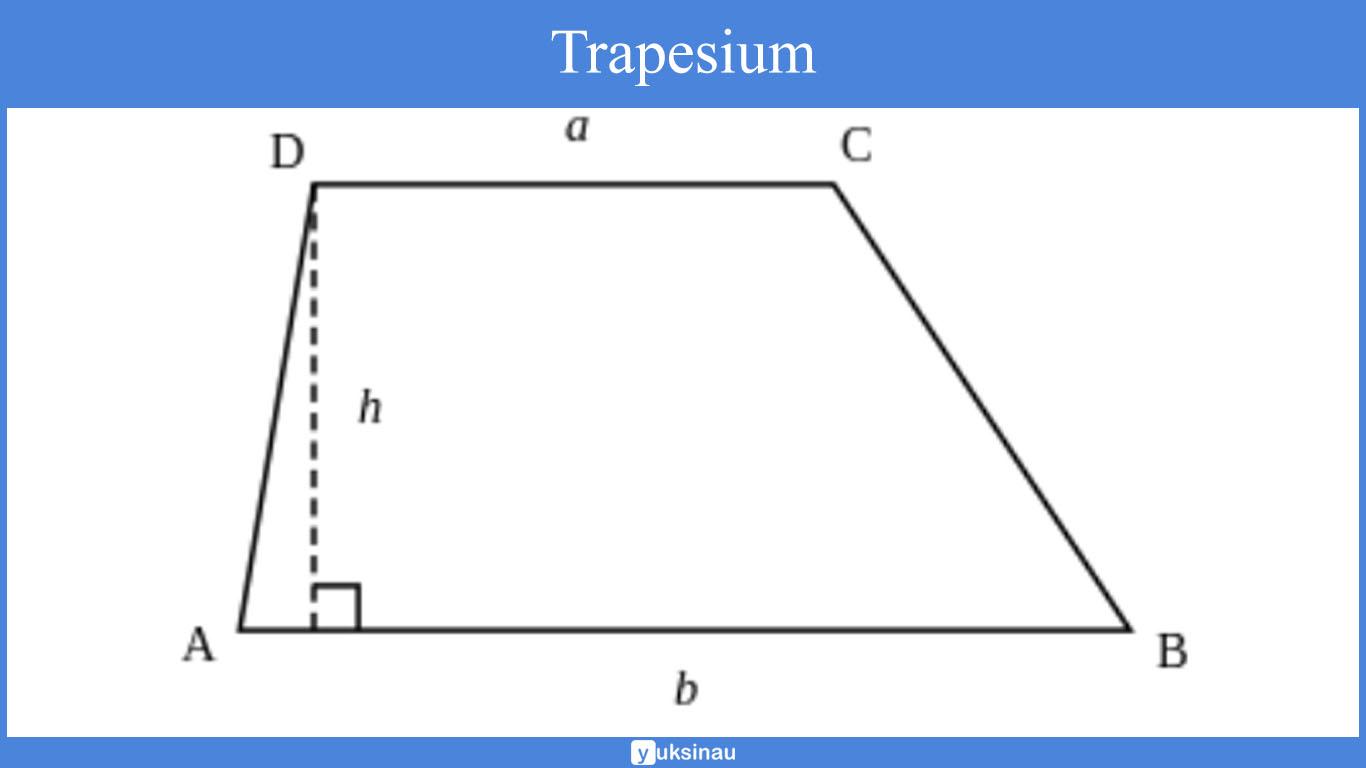
Sifat umum trapesium:

1. Mempunyai sepasang sisi berhadapan sejajar (AB // DC)
2. Jumlah sudut yang berdekatan di antara dua sisi sejajar yaitu 180^o
   ∠A + ∠D = ∠B + ∠C = 180^o

a. Trapesium Sama Kaki

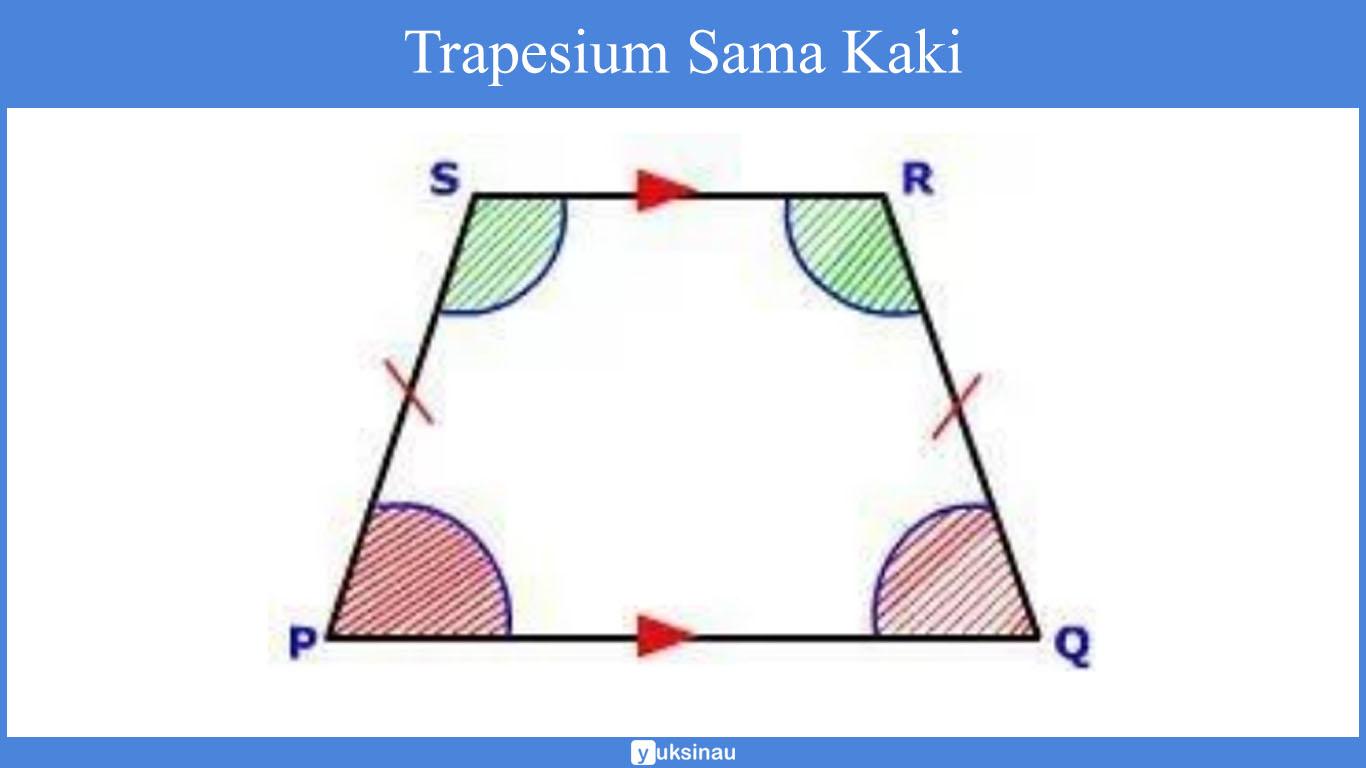
Sifat trapesium sama kaki:

1. Dua sudut alas sama besar yaitu ∠P = ∠Q
2. Dua sudut pada sisi atas sama besar  yaitu ∠S = ∠R
3. Dua diagonal sama panjang

b. Trapesium Siku Siku

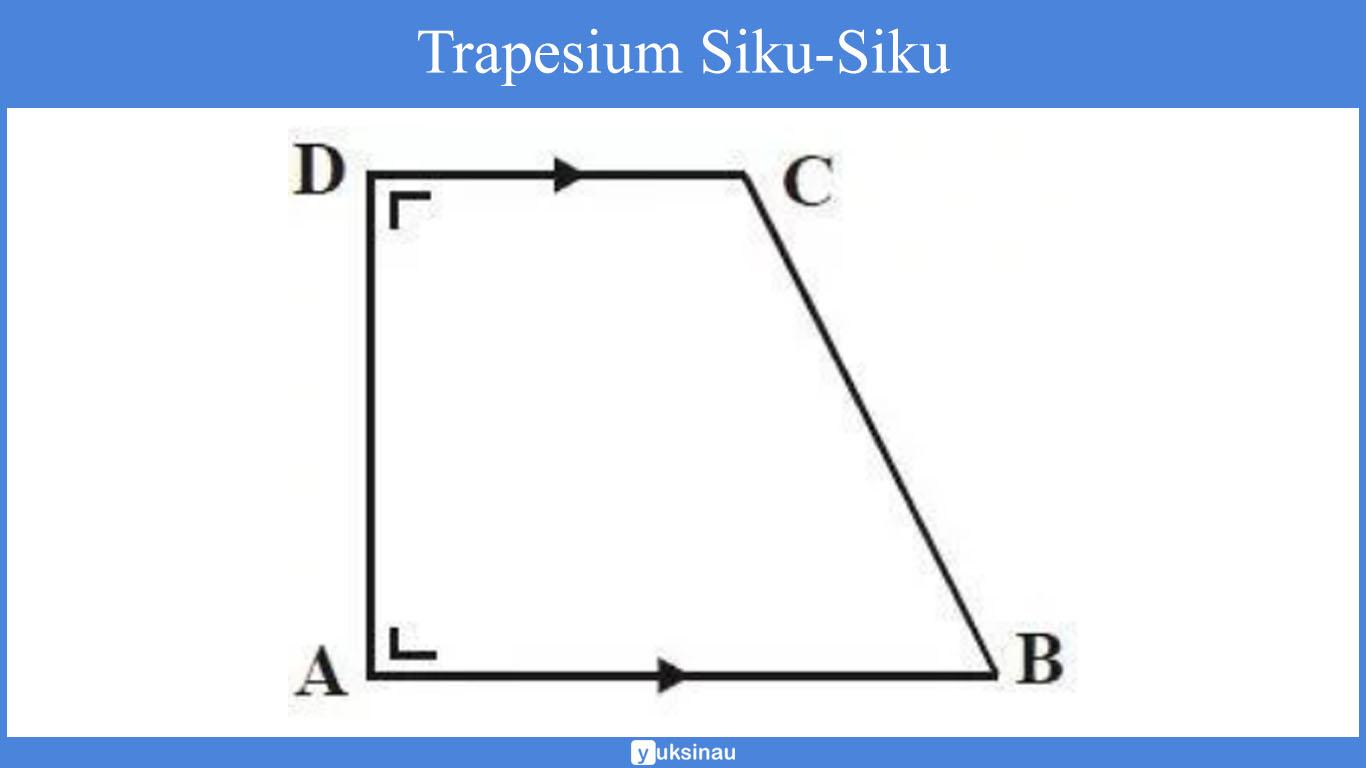
Sifat trapesium sama siku siku:

1.  Mempunyai tepat dua sudut siku-siku yaitu ∠A dan ∠D

Rumus trapesium:

• Luas: L = ½ x (AB + DC) x t = ½ x Jumlah sisi yang sejajar x tinggi
• Keliling: K = AB + BC + CD + DA = Jumlah semua sisi

E. Belah Ketupat

Belah ketupat merupakan suatu bangun datar dua dimensi yang dibentuk oleh empat buah rusuk yang memiliki panjang yang sama.

Serta mempunyai dua pasang sudut bukan siku-siku yang mana pada masing-masing sudutnya sama besar dengan sudut di hadapannya.

Belah ketupat bisa dibangun dari dua buah segitiga sama kaki identik yang simetri pada alas-alasnya. Sebagai conoh yaitu ketupat, seperti banyak kalian jumpai pada waktu membeli ketupat sayur ataupun ketoprak.

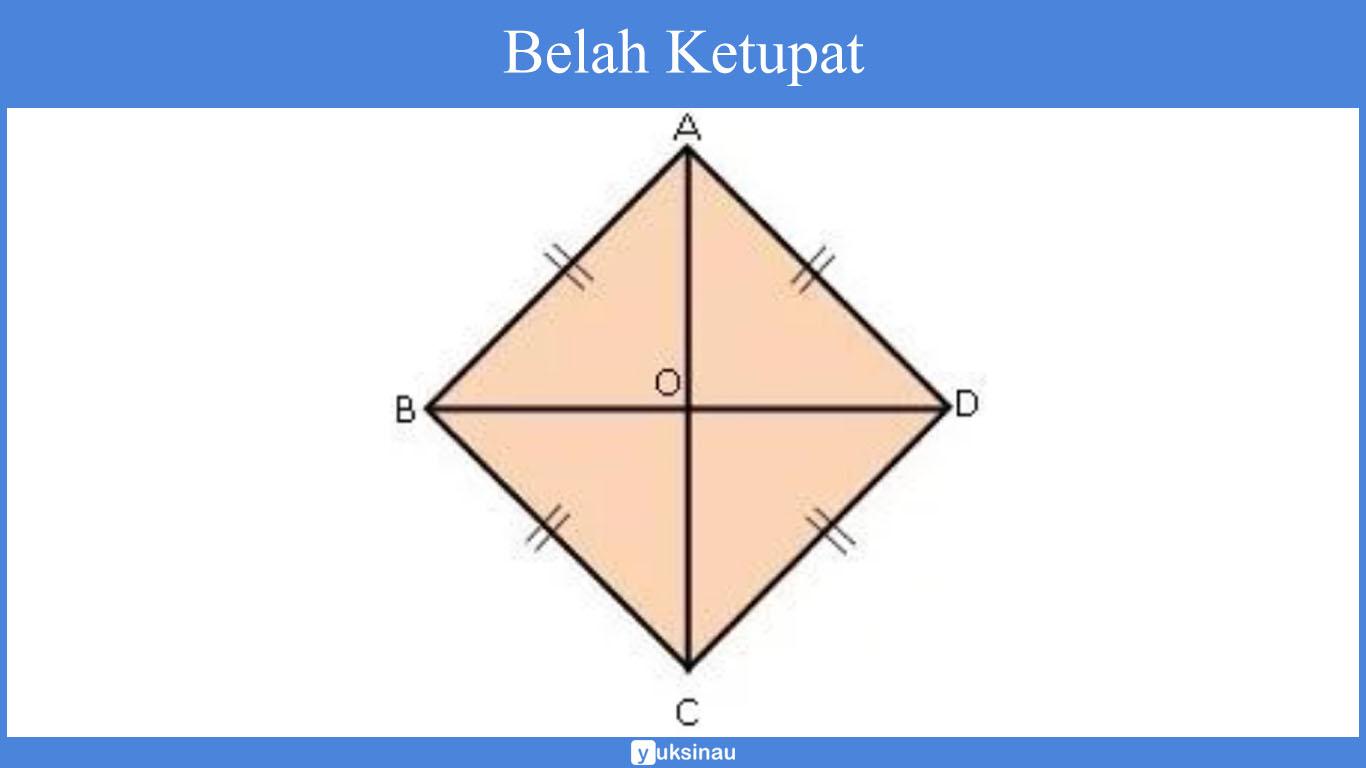
Sifat belah ketupat:

1. Keempat sisinya sama panjang dan juga berpasangan sejajar (AB = BC = CD = DA dan AB // DC dan BC // AD)
2. Kedua diagonal berpotongan tegak lurus serta saling membagi sama panjang (AC = BD serta AO = OC, BO = OD)
3. Sudut-sudut yang berhadapan sama besar serta terbagi dua sama besar oleh diagonal-diagonalnya, yaitu: ∠A = ∠C , ∠B = ∠D

Rumus belah ketupat:

• Diagonal: d
• Sisi-sisi: s
• Luas: L = ½ x d1 x d2 = ½ x AC x BD
• Keliling: K = 4 x s

F. Layang-layang

Layang-layang merupakan sebuah bangun datar dua dimensi yang dibentuk oleh dua pasang rusuk yang mana pada masing-masing pasangannya sama panjang serta saling membentuk sudut.

Layang-layang hanya mempunyai satu sumbu simetri, dan juga satu sudut yang sama besar. Sebagai contoh yaitu layangan.

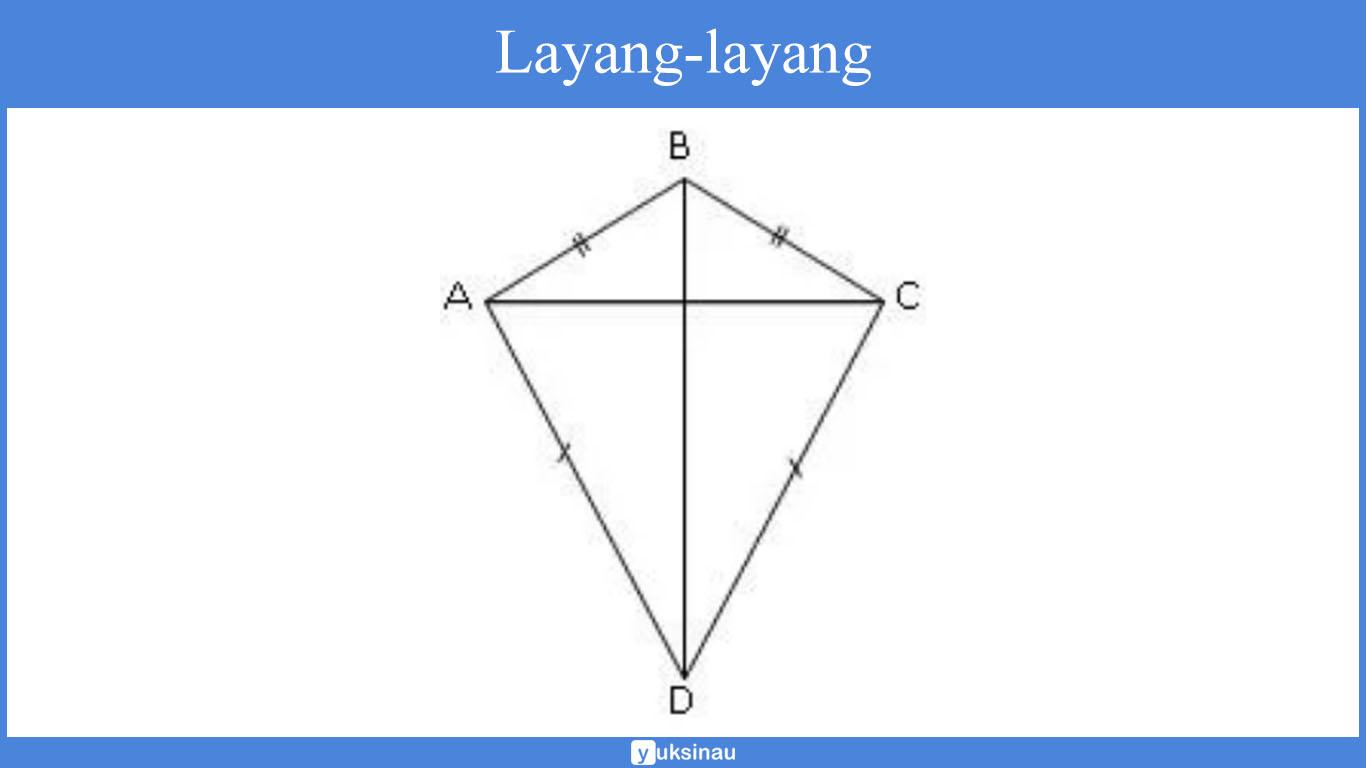
Sifat layang-layang:

1. Memiliki dua pasang sisi yang salaing berdekatan sama panjang (AD = DC dan AB = BC)
2. Dua diagonalnya saling tegak lurus serta yang satu membagi dua yang lain sama panjang (AC ⊥ BD serta AT = TC)
3. Mempunyai sepasang sudut yang berhadapan sama besar yaitu ∠BAD = ∠BCD
4. Mempunyai sebuah diagonal (BD) yang membagi dua sudut sama besar yaitu ∠ADB = ∠BDC dan ∠ABD = ∠CBD.

Rumus layang-layang:

• Diagonal: d
• Luas: L = ½ x d1 x d2 = ½ x BD x AC
• Keliling = K = AB + BC + CD + DA = 2(AB + CD) = Jumlah semua sisi

Contoh Soal dan Pembahasan

Soal 1.

Apabila diketahui panjang sebuah persegi adalah 5 cm. Maka hitungah luas dan keliling persegi tersebut!

Jawab:

Keliling = s + s + s + s atau 4 xs = 5 cm + 5 cm +5 cm + 5 cm = 20 cm

Luas = s x s= 5 x 5 = 25 cm²

Soal 2.

Apabila diketahui keliling dari sebuah persegi yaitu 24 cm. Maka hitunglah Luas persegi tersebut!

Jawab:

Untuk mencari Luas, maka langkah petama adalah mengetahui terlebih dahulu sisi persegi tersebut dengan memakai rumus keliling, sehingga akan menjadi:

Keliling = 4 x s
24 cm   = 4 x s
s           = 24 cm/4
s           = 6 cm

Kemudian kita masukkan rumus luas persegi!

Luas = s x s = 6 cm x 6 cm = 36 cm²

Soal 3.

Hitunglah keliling dan luas dari persegi panjang di bawah ini!

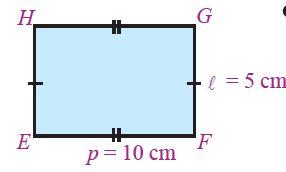
Jawab:

K = p + l + p + l = 10 cm + 5 cm + 10 cm + 5 cm = 30 cm

L = p x l = 10 cm x 5 cm = 50 cm²

Soal 4.

Diketahui sebuah bangun jajargenjang memiliki alas 7 cm dan tinggi 4 cm. Tentukan luas jajargenjang tersebut!

Jawab:

L = a x t = 7 cm x 4 cm = 28 cm²

Soal 5.

Sebuah bangun jajargenjang mempunyai keliling 52 cm. Apabila panjang salah satu sisinya yaitu 16 cm, maka hitunglah panjang sisi yang lainnya!

Jawab:

Dari soal di atas, telah kita ketahui bahwa kelilingnya adalah = 52 cm serta panjang salah satu sisi yang diketahui 16 cm (misalnya a).

Sehingga untuk mengetahui panjang sisi yang lain (misalnya t) yang belum diketahui bisa dicari dengan memakai rumus keliling!

Keliling = 2 x (a x t)
52 cm   = 2 x (16 cm x t)
52 cm   = 32 cm x 2t
52 cm – 32 cm = 2t
2t = 20
t   = 20/2
t   = 10 cm.

Soal 6.

Diketahui panjang diagonal-diagonal pada sebuah belah ketupat berturut-turut yaitu 15 dan 12. Hitunglah luas belah ketupat tersebut!

Jawab:

L = 1/2 x d1 x d2 = 1/2 x 15 x 12 = 90 cm²

Soal 7.

Panjang diagonal-diagonal pada sebuah belah ketupat berturut-turut yaitu 18 cm dan (2x + 3) cm. Apabila diketahui luas belah ketupat tersebut adalah 81 cm^2, maka hitunglah nilai x serta panjang diagonal yang kedua.

Jawab:

L = 1/2 x d1 x d2
81 cm² = 1/2 x 18 cm (2x + 3) cm
81 cm² = 9 cm (2x + 3) cm
81 cm² = 18x cm² + 27 cm²
81 cm² – 27 cm² = 18x cm²
54 cm² =18x cm²
x = 54 cm² /18 cm²
x = 3

Soal 8.

Perhatikan gambar bangun layang-layang PQRS di bawah ini!

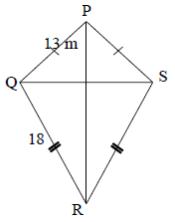
Apabila diketahui ∠PQR merupakan siku-siku, hitunglah luas layang-layang PQRS tersebut!

Jawab:

Disebabkan ∠PQR siku-siku, maka luas dari bangun layang-layang PQRS di atas bisa kita cari dengan memakai rumus luas segitiga.

Dengan alasnya = QR = 18 m serta tinggi = PQ = 13 m.

Dari layang-layang PQRS terdapat dua segitiga siku-siku yakni ΔPQR dan ΔPSR dengan luas yang sama. Oleh sebab itu luas layang-layang bisa kita cari dengan menjumlahkan dua luas segitiga siku-siku.

Luas PQRS = Luas ΔPQR + Luas ΔPSR
Luas PQRS = 2 x Luas PQR (karena luas PQR dan PSR sama)
Luas PQRS = 2 x 1/2 x 18 m x 13 m
Luas PQRS = 234 m²

Soal 9.

Suatu bangun trapesium mempunyai sisi sejajar masing-masing 10 cm serta 12 cm. Hitunglah luas trapesium tersebut apabila tinggi trapesiumnya 8 cm.

Jawab:

L = 1/2 x jumlah rusuk sejajar x tinggi
L = 1/2 x (10 cm + 12 cm) x 8 cm
L = 1/2 x 22 cm x 8 cm
L = 88  cm²

Soal 10.

Perhatikan gambar bangun di bawah ini!

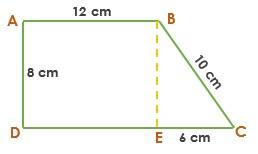
Tentukan keliling dan juga luas trapesium di atas!

Jawab:

Perhatikan gambar di atas. Pada ABED merupakan bangun persegi panjang sehingga, panjang dari sisi ED = AB = 12 cm. Maka dari itu,

Keliling = AB + BC + CE + ED + AD = 12 cm + 10 cm + 6 cm + 12 cm + 8 cm = 48 cm

Luas = 1/2 x jumlah rusuk sejajar x tinggi
Luas = 1/2 x (12 cm + 18 cm) x 8 cm
Luas = 1/2 x 30 cm x 8 cm
Luas = 120 cm²

Soal 11.

Perhatikan gambar trapesium di bawah ini!

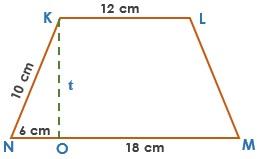
Hitunglah keliling dan juga luas trapesium KLMN tersebut!

Jawab:

K = NK + KL + LM + MN = 10 cm + 12 cm + 10 cm + (18 cm + 6 cm) = 56 cm

Untuk mencari luas trapesium KLMN di atas, maka kita harus mengetahui terlebih dahulu tingginya. Sementara untuk mencari tinggi bisa ditemukan dengan memakai rumus phytagoras.

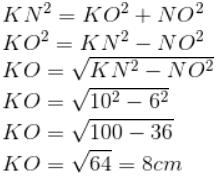
KO merupakan tinggi trapesium = 8 cm, sehingga:

Luas = 1/2 x jumlah ruas sejajar x tinggi
Luas = 1/2 x (12 cm + 24 cm) x 8 cm
Luas = 144 cm²

Soal 12.

Perhatikan gambar bangun layang-layang di bawah ini!

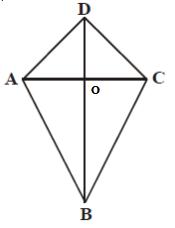
Apabila diketahui panjang AC = 24 cm, BC = 20 cm, serta luas ABCD = 300 cm², hitung panjang AD dan juga keliling layang-layang ABCD di atas!

Jawab:

Luas = 1/2 x d1 x d2
Luas = 1/2 x AC x BD
300 cm² = 1/2 x 24 cm x BD
300 cm² = 12 cm x BD
BD = 300 cm²/12 cm
BD = 25 cm

Kemudian mencari BO terlebih dahulu dengan cara memakai rumus phytagoras.

BO = √(BC² – CO²)
BO = √(20² – 12²)
BO = √(400 – 144)
BO = √256
BO = 16 cm

Berikutnya mencari panjang DO, yaitu:

DO = BD – BO
DO = 25 cm – 16 cm
DO = 9 cm

Nah, sekarang AD bisa kita cari dengan memakai rumus phytagoras,

AD = √(AO² – DO²)
AD = √(12² – 9²)
AD = √(144 – 81)
AD = √225
AD = 15 cm

Sementara untuk mencari keliling layang-layang ABCD, yaitu:

Keliling = 2 (AD + BC)
Keliling = 2 (15 cm + 20 cm)
Keliling = 2 x 35 cm
Keliling = 70 cm

Baca juga: Segitiga

Demikianlah ulasan singkat kali ini mengenai segiempat yang dapat kami sampaikan. Semoga ulasan di atas mengenai segiempat dapat kalian jadikan sebagai bahan belajar kalian.

The post Segiempat appeared first on Tuliskan.

ARTIKEL PILIHAN PEMBACA :

Memuat...

Ketika Anda membaca kalimat ini, berarti Anda sudah sampai dibagian akhir dari pembahasan tentang Segiempat - Poin 100. Besar harapan kami ulasan yang kami sampaikan diatas bisa menjadi sarana pembelajaran untuk kita semua, terutama untuk Anda yang memang sedang mencarinya. Tak lupa kami sampaikan banyak terima kasih karena sudah berkunjung ke situs poin100. blogspot. com dan membaca hingga selesai. Salam santun dan sampai ketemu di artikel selanjutnya.