Himpunan Matematika - Poin 100
Keberadaan internet membuat siapa saja bisa mengakses berbagai informasi, maka tidak heran belakangan ini banyak sekali betebaran situs-situs yang membahas mengenai Himpunan Matematika. Hal ini sangat logis mengingat di era pandemi ini, masyarakat kita lebih sering melakukan proses belajar mengajar secara daring. Baiklah sudah cukup basa-basinya, yuk langsung masuk ke pembahasan saja.
Penjelasan Lengkap Himpunan Matematika
Himpunan Matematika merupakan suatu kumpulan benda atau objek yang dapat diartikan dengan jelas, sampai kita bisa dengan tepat mengetahui objek yang termasuk himpunan serta yang tidak termasuk dalam himpunan tersebut.
Sebuah Himpunan Matematika biasanya dilambangkan dengan menggunakan huruf kapital seperti: A, B, C, D, E, …………….. Z, benda maupun objek yang termasuk kedalam himpunan disebut anggota himpunan. Serta elemen himpunan ditulis dengan menggunakan sepasang kurung kurawal {……..}
Jenis Jenis Himpunan Matematika
1. Himpunan Matematika Semesta
Himpunan semesta atau juga disebut dengan semesta pembicaraan merupakan himpunan yang memuat seluruh anggota maupun objek himpunan yang dibicarakan.
Himpunan semesta (semesta pembicaraan) pada umumnya dilambangkan dengan menggunakan huruf S atau U.
Sebagai contoh:
Jika kita membahas tentang 1, ½, -2, -½,… maka semesta pembicaraan kita merupakan bilangan real.
Sehingga himpunan semesta yang dimaksud yaitu R.
Apakah hanya R saja?
Tentu saja tidak. Tergantung kita ingin membatasi pembicaraanya.
Pada contoh di atas dapat kita katakan semestanya merupakan C (himpunan bilangan kompleks). Tetapi kita tidak dapat mengambil Z (himpunan bilangan bulat) sebagai semesta pembicaraan.
2. Himpunan Matematika Kosong
Himpunan kosong merupakan suatu himpunan yang tidak memiliki anggota. Serta dinotasikan dengan menggunakan {} atau ∅.
Himpunan nol merupakan himpunan yang hanya memiliki l anggota, yakni nol (0).
3. Himpunan Matematika Bagian
Himpunan A adalah suatu himpunan bagian B, apabila pada masing-masing anggota A juga menjadi anggota B serta dinotasikan dengan A ⊂ B atau B ⊃ A.
Apabila terdapat himpunan A dan B di mana pada masaing-masing anggota A adalah anggota B, maka disebutkan bahwa A adalah himpunan bagian (subset) dari B atau disebut sebagai B memuat A serta dilambangkan dengan simbol A ⊂ B.
Sehingga, A ⊂ B jika dan hanya apabila ? ⊂ A ⇒ ? ⊂ B
Apabila terdapat anggota dari A yang bukan bagian dari anggota B, maka A bukan bukan merupakan himpunan bagian dari B. Serta dilambangkan dengan menggunakan simbol A ⊄ B.
4. Himpunan Matematika Sama (Equal)
Jika masing-masing anggota himpunan A juga bagian dari anggota himpunan B, begitu juga sebaliknya maka dinotasikan dengan A=B
Syarat:
Dua buah himpunan anggotanya harus sama.
Sebagai contoh:
A ={ c,d,e} B={ c,d,e } Maka A = B
Keterangan:
Himpunan equal atau himpunan sama mempunyai dua buah himpunan yang di mana anggotanya sama. Contohnya pada anggota himpunan A {c,d,e} maka himpunan B pun akan mempunyai anggota yakni { c,d,e }.
5. Himpunan Matematika Lepas
Himpunan lepas merupakan sebuah himpunan yang di mana setiap anggotanya tidak ada yang sama.
Sebagai contoh:
C = {1, 3, 5, 7} serta D = {2, 4, 6} Maka himpunan C dan juga himpunan D saling lepas.
Catatan:
Dua himpunan yang tidak kosong disebut saling lepas apabila kedua himpunan tersebut tidak memiliki satu pun anggota yang sama
6. Himpunan Matematika Komplemen (Complement set)
Himpunan komplemen bisa dinyatakan dengan menggunakan notasi AC .
Himpunan komplemen apabila diibaratkan akan menjadi: S = {1,2,3,4,5,6,7} dan A = {3,4,5} maka A ⊂ U.
Himpunan {1,2,6,7} pula merupakan komplemen, sehingga menjadi AC = {1,2,6,7}.
Dengan penggunaan notasi pembentuk himpunan maka ditulis menjadi:
AC = {x│x Є U, x Є A}
7. Himpunan Matematika Ekuivalen (Equal Set)
Himpunan ekuivalen merupakan suatu himpunan yang di mana setiap anggotanya sama banyak dengan himpunan lain.
Syarat:
Bilangan cardinal dinyatakan dengan menggunakan notasi n (A) A≈B, disebut sebagai sederajat atau ekivalen, apabila himpunan A ekivalen dengan himpunan B,
Sebagai contoh:
A = { w,x,y,z }→n (A) = 4
B = { r,s,t,u } →n (B) = 4
Sehingga n (A) =n (B) →A≈B
Keterangan:
himpunan ekivalen memiliki bilangan cardinal dari himpunan itu jika himpunan A beranggotakan 4 karakter sehingga himpunan B juga beranggotakan 4.
Cara Menyatakan Himpunan
Himpunan bisa kita nyatakan dengan melalui tiga cara, antara lain:
1. Dengan kata-kata
Merupakan cara menyatakan himpunan dengan menyebutkan seluruh syarat maupun sifat-sifat keanggotaan dari sebuah himpunan.
Sebagai contoh:
A merupakan himpunan bilangan asli antara 5 dan 12, maka kita tuliskan menjadi A = {bilangan asli antara 5 dan 12}
2. Dengan Notasi Pembentuk Himpunan
Merupakan cara menyatakan himpunan dengan menyebutkan seluruh syarat atau sifat ke-anggotaan dari sebuah himpunan. Tetapi anggota himpunan disebutkan dalam variabel peubah.
Sebagai contoh:
A merupakan himpunan bilangan asli antara 5 dan 12, sehingga kita tuliskan menjadi: {x: 5<x<12,x bilangan asli}.
3. Dengan Mendaftar Anggota-anggotanya
Yakni cara menyatakan himpunan dengan menuliskan anggota-anggota himpunan dalam pasangan kurung kurawal serta memisahkannya dengan menggunakan tanda koma.
Sebagai contoh:
A merupakan himpunan bilangan asli antara 5 dan 12, sehingga kita tulis menjadi: A= {6,7,8,9,10,11}
Operasi Himpunan
1. Irisan Himpunan
Irisan dari dua himpunan A dan B merupakan himpunan yang di mana setiap anggotanya terdapa di himpunan A dan juga terdapat di dalam himpunan B.
Dengan kata lain yakni himpunan yang anggotanya terdapat di kedua himpunan tersebut.
Sebagai contoh:
A = {a, b, c, d, e} dan B = {b, c, f, g, h}
Pada kedua himpunan di atas terdapat dua anggota yang sama yakni b dan c. Oleh sebab itu, bisa dinyatakan bahwa irisan himpunan A dan B merupakan b dan c atau ditulis dengan:
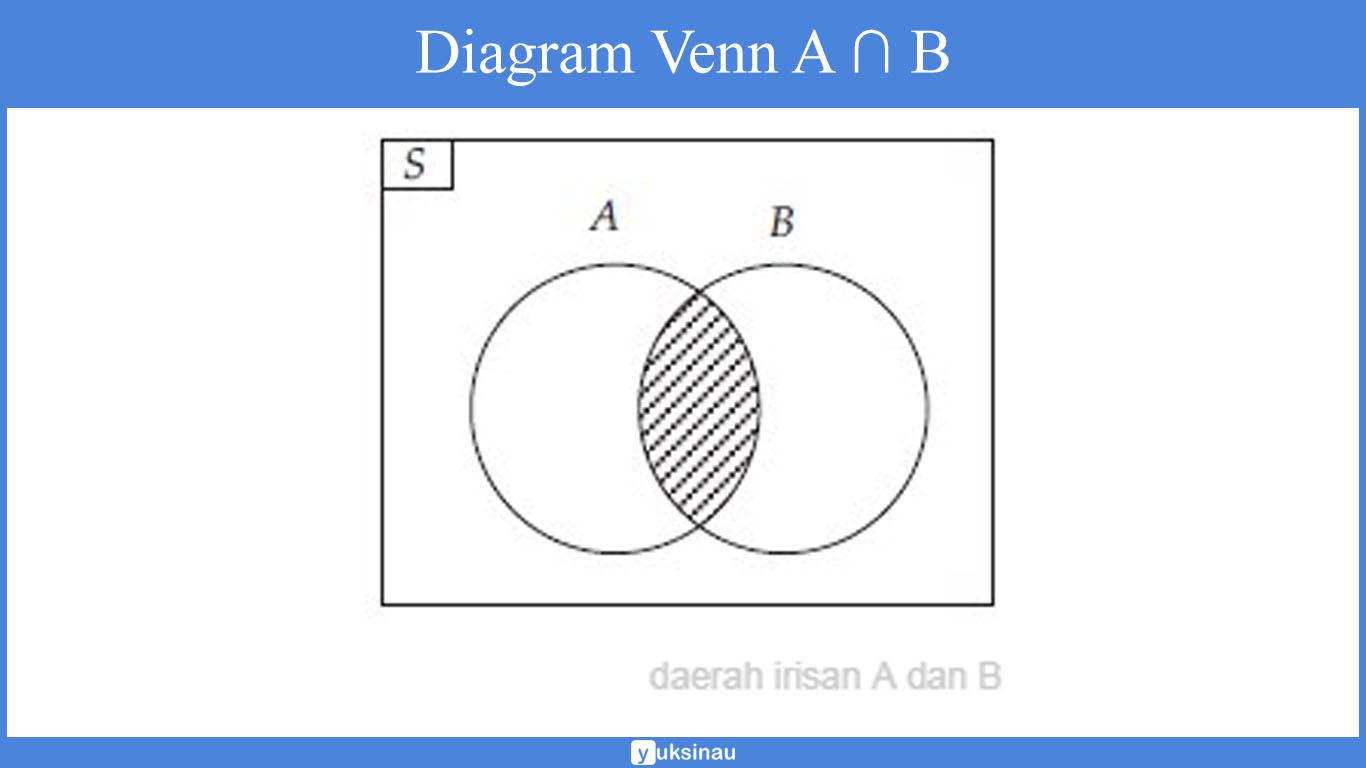
A ∩ B = {b, c}
A ∩ B dibaca: himpunan A irisan himpunan B. Dengan diagram Venn A ∩ B juga bisa dinyatakan seperti pada gambar di bawah ini:
2. Gabungan Himpunan
A gabungan B ditulis menjadi:
A ∪ B = {x | x ∈ A atau x ∈ B}
Sebagai contoh:
A = {1, 2, 3, 4, 5}
B = {2, 3, 5, 7, 11}
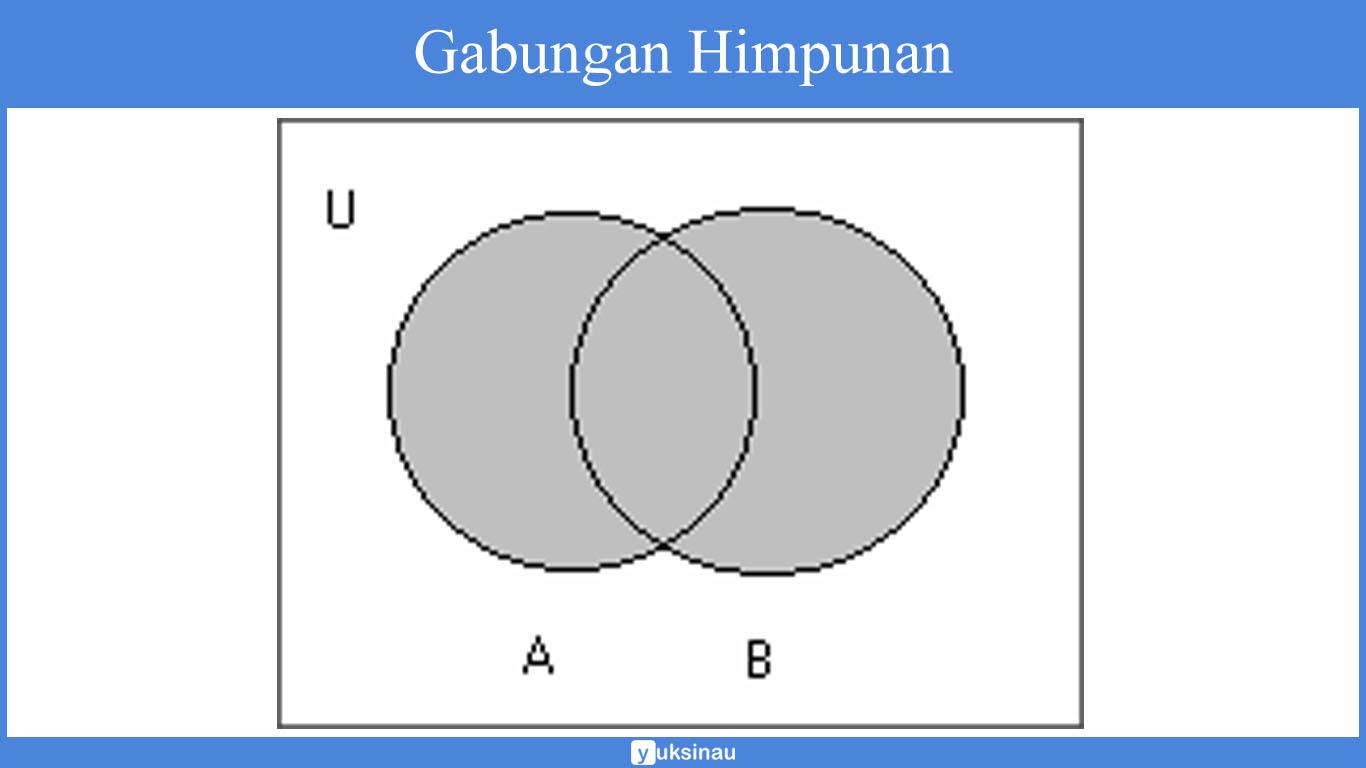
A ∪ B = {1, 2, 3, 4, 5, 7, 11}
Apabila dinyatakan dalam bentuk diagram Venn maka:
3. Selisih
A Selisih B ditulis menjadi: A-B = {x | x ∈ A atau x Ï B}
Sebagai contoh:
A = {1, 2, 3, 4, 5}
B = {2, 3, 5, 7, 11}
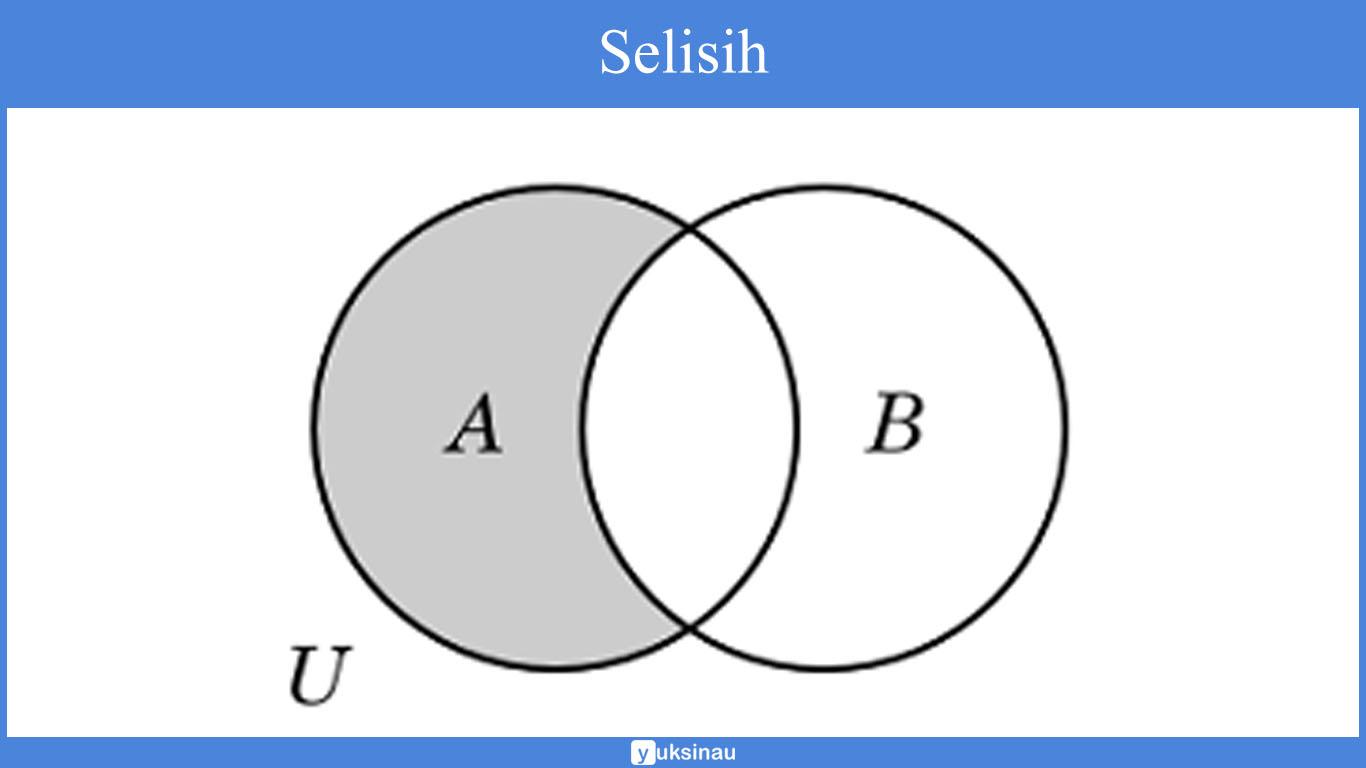
A-B = {1, 4}
Apabila dinyatakan dalam bentuk diagram Venn maka:
4. Komplemen Himpunan
Komplemen A ditulis menjadi A1 atau Ac = {x | x ∈ S dan x Ï A}
Sebagai contoh:
A= {1, 2, … , 5}
S = {biangan Asli kurang dari 10}
Ac = {6, 7, 8, 9}
Apabila dinyatakan dalam bentuk diagram Venn maka:

Contoh komplemen:
- Contohnya U = { 1, 2, 3, …, 9 },
- Apabila A = {1, 3, 7, 9}, maka Ā = {2, 4, 5, 6, 8}
- Apabila A = { x ∈ U | x habis dibagi dua }, maka A= { 1, 3, 5, 7, 9 }
a. Pernyataan
“Seluruh mahasiswa ITT Telkom angkatan 2017 yang membawa motor untuk pergi ke kampus” bisa kita nyatakan dalam notasi operasi himpunan seperti berikut ini:
(A ∩ C) ∩ E
b. Pernyataan
“Seluruh mahasiswa ITT Telkom yang tinggal di asrama serta tidak mengambil matematika diskrit” bisa kita nyatakan dalam notasi operasi himpunan seperti berikut ini:
A ∩ B ∩ D
c. Pernyataan
“Seluruh mahasiswa angkatan 2017 yang tidak tinggal di asrama atau tidak membawa motor untuk pergi ke kampus” bisa kita nyatakan dalam notasi operasi himpunan seperti berikut ini:
C ∩ (B ∪ E)
5. Beda setangkup (SYMMETRIC DIFFERENCE)
Beda setangkup antara dua buah himpunan dinotasikan dengan penggunakan tanda atau simbol ‘⊕‘.
Sebagai contoh:
A dan B merupakan himpunan, maka beda setangkup antara A dan B dinotasikan menjadi:
A ⊕ B = (A ∪ B) – (A ∩ B)
= (A – B) ∪ (B – A)
Dan apabila dinyatakan dalam bentuk diagram Venn akan menjadi:
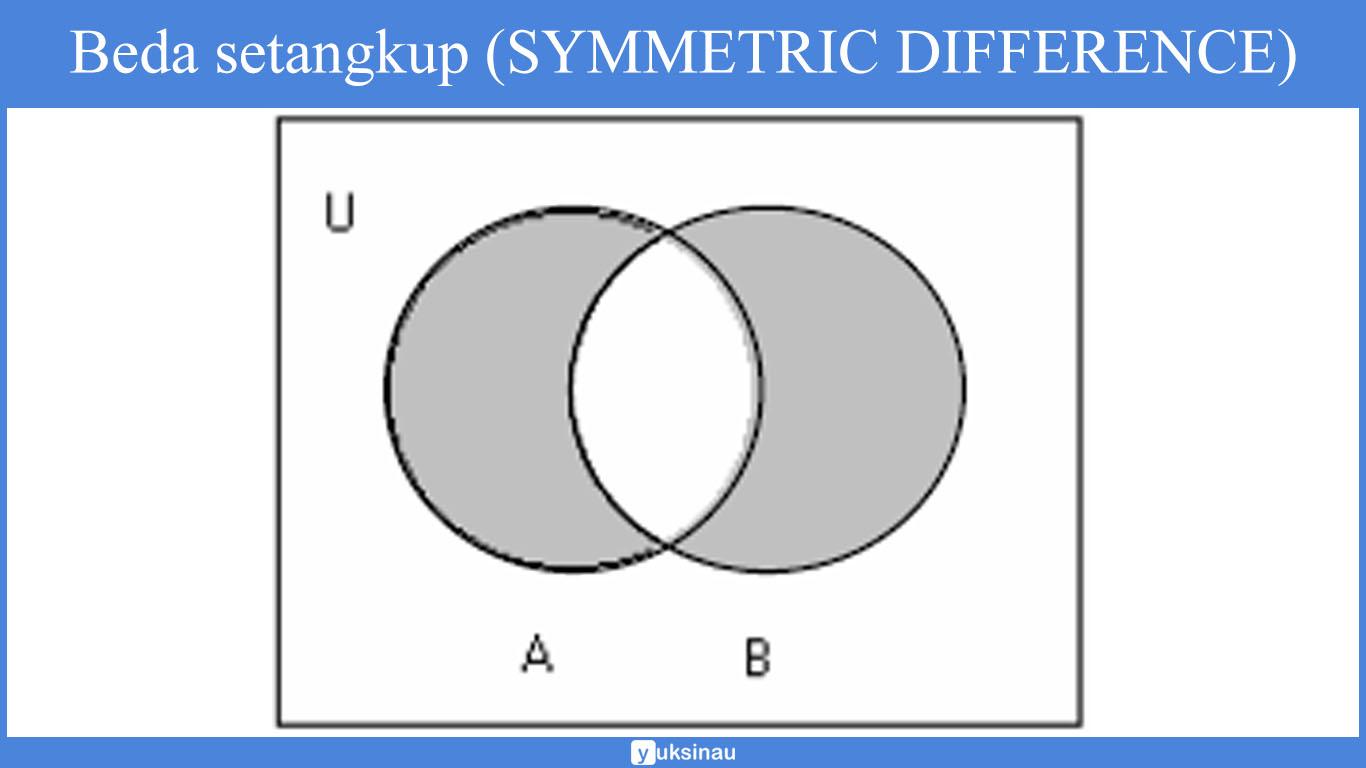
Contoh beda setangkup:
Apabila A = { 2, 3, 5, 7} serta B = { 1, 2, 3, 4, 5 }, maka A ⊕ B = { 1, 4, 7 }
Beda setangkup memenuhi sifat-sifat berikut:
- A ⊕ B = B ⊕ A (hukum komutatif)
- (A ⊕ B ) ⊕ C = A ⊕ (B ⊕ C ) (hukum asosiatif)
Contoh Soal dari Operasi Himpunan
Apabila diketahui:
A= {1, 2, 3, 4, 5}
B = {2, 3, 6, 7, 8}
C = {4, 5, 6, 7, 8}
Maka tentukanlah:
a. A ∩ B
c. B ∩ C
b. A ∩ C
d. A ∩ B ∩ C
Jawab:
a. A ∩ B = {2, 3}
c. B ∩ C = {6, 7, 8}
b. A ∩ C = {4, 5}
d. A ∩ B ∩ C = { }
Diagram Venn
Diagram venn merupakan menyajikan sebuah himpunan dengan satu himpunan dengan menggunakan lingkaran serta semua himpunan atau himpunan semesta yang digambarkan dengan menggunakan gambar segi empat.
Macam Macam Himpunan
- Himpunan bilangan asli: A = { 1, 2, 3, 4, 5, … }
- Himpunan bilangan cacah: C = { 0, 1, 2, 3, 4, …. }
- Himpunan bilangan prima: P = { 2, 3, 5, 7, 11, …. }
- Himpunan bilangan genap: G = { 0, 2, 4, 6, 8, 10, …. }
- Himpunan bilangan ganjil: G = { 1, 3, 5, 7, 9, …. }
- Himpunan bilangan komposit (tersusun): T = { 4, 6, 8, 9, 10, 12, …. }
- Himpunan tak hingga: A = { 1, 3, 5, 7, ….. }, (n)A = ∞ (jumlah anggota himpunan A yaitu tak terhingga)
- Himpunan berhingga: B = { 1, 3, 5, 7 }, (n)A = 4 (jumlah anggota himpunan B yaitu sebanyak 4)
- Himpunan kosong: K = { himpunan bilangan prima antara 7 dan 9 }, K = { } (jumlah anggota himpunan K yaitu tidak ada atau kosong)
- Himpunan bagian: A = {2, 3, 5 } dan B = { 1, 2, 3, 4, 5, 6 }
Seluruh anggota himpuna A merupakan anggota himpunan B. Sehingga bisa dikatakan bahwa; A bagian dari B, ditulis A c B atau B mencangkup A ditulis B ﬤ A - Himpunan semesta
Jika A = { 2, 4, 6, 8, 10 }, maka beberapa himpunan semesta pembicaraan yang mungkin untuk A yaitu;
S = { bilangan asli }
S = { bilangan cacah }
S = { bilangan kelipatan 2 }
Himpunan Penyelesaian Sistem Persamaan Linear Dua Variabel (SPLDV)
Untuk mencari himpunan penyelesaian dari suatu sistem persamaan linear dua variabel dapat kita lakukan dengan menggunakan empat metode atau cara, diantaranya yaitu:
- Metode grafik
- Metode substitusi
- Metode eliminasi
- Metode campuran (substitusi dan eliminasi).
Apabila terdapat dua buah persamaan liniear dua variabel yang berbentuk ax + by = c dan px + qy = r, dimana persamaan yang satu dan yang lainnya tidak terpisahkan, maka persamaan-persamaan itu disebut sebagai sistem persamaan linear dua variabel.
Adapaun entuk umum dari sistem persamaan linear dua variabel, yakni:
ax + by = c
px + qy = r
Dalam sistem persamaan linear dua variabel (SPLDV) a, b, p, dan q disebut sebagai koefisien, x serta y merupakan variabel dari SPLDV, sementara c dan r disebut sebagai konstanta.
Selengkapnya mengenai SPLDV silahkan kunjungi Sistem Persamaan Linear Dua Variabel (SPLDV).
Metode Grafik
Pada saat menggunakan metode grafik, kita wajib untuk menggambar tiap-tiap persamaan linear dua variabel dalam koordinat kartesius.
Himpunan penyelesaiannya adalah titik potong dari kedua garis yang digambar.
Apabila garisnya tidak saling berpotongan atau sejajar. Maka himpunan penyelesaiannya merupakan himpunan kosong.
Namun apabila garisnya salaing berhimpit maka jumlah himpunan penyelesaiannya tak berhingga.
Metode Subtitusi
Berikut adalah tahapan untuk memakai metode substitusi dalam mencari himpunan penyelesaian dari SPLDV, diantaranya adalah sebagai berikut:
- Ubahlah salah satu persamaan ke dalam bentuk x = … atau y = …
- Masukkan (substitusi) nilai x atau y yang diperoleh ke dalam persamaan yang kedua
- Nilai x atau y yang diperoleh kemudian disubstitusikan ke dalam salah satu persamaan untuk mendapatkan nilai variabel lainnya yang belum diketahui (x atau y).
Metode Eliminasi
Penyelesaian SPLDV dengan penggunaan metode eliminasi pada dasarnya adalah menghilangkan (mengeliminasi) salah satu dari variabel sistem persamaan yang akan kita cari himpunan penyelesaiannya.
Caranya cukup mudah yakni dengan cara menjumlahkan maupun mengurangkan kedua sistem persamaan tersebut.
Untuk menentukan variabel y, maka kita harus menghilangkan terlebih dahulu variabel x.
Begitu pula sebaliknya, untuk mencari variabel x, maka kita harus menghilangkan variabel y terlebih dahulu.
Catatan:
Untuk menghilangkan variabel x atau y maka koefisien dari tiap-tiap variabel dalam sistem persamaan harus sama.Apabila salah satu variabelnya tidak sama maka harus disamakan terlebih dahulu. Caranya cukup dengan mengalikan variabel tersebut dengan bilangan bulat tertentu sehingga koefisiennya akan menjadi sama.
Metode Campuran (Eliminasi dan Substitusi)
Dalam prumusan soal persamaan linear dua variabel, tak jarang kita menjumpai kesulitan apabila dengan memakai metoda eliminasi untuk menentukan himpunan penyelesaiannya.
Oleh karena itu, kita dapat memakai metode campuran. Metode campuran adalah metoded dengan cara menentukan salah satu variabel x atau y dengan memakai metode eliminasi.
Hasil yang kita dapatkan dari x atau y selanjutnya kita substitusikan ke salah satu persamaan linear dua variabel tersebut.
Contoh Soal dan Pembahasan
Soal 1.
Dari 28 orang siswa yang mengikuti kegiatan ekstrakurikuler di sekolah serta masing-masing siswa tersebut berjumlah 15 orang siswa yang mengikuti pramuka. Kemudian 12 orang siswa mengikuti futsal. Serta yang terakhir 7 orang siswa yang mengikuti keduanya.
Maka hitunglah berapa banyak siswa yang tidak mengikuti ekstrakurikuler pramuka ataupun ekstrakurikuler futsal ialah?
Jawab:
Misalkan ( x ) merupakan banyak siswa yang tidak mengikuti ekstrakurikuler.
Banyak anak yang hanya mengikuti ekstrakurikuler pramuka adalah sebanyak 15 – 7 = 8 orang siswa.
Banyak anak yang hanya mengikuti ekstrakurikuler futsal adalah sebanyak 12 – 7 = 5 orang siswa.
Maka himpunan tersebut bisa kita gambarkan dengan menggunakan bentuk diagram venn seperti gambar yang ada di bawah ini :
Banyak anak yang tidak mengikuti ekstrakurikuler adalah:
8 + 7 + 5 + x = 28
20 + x = 28
x = 28 – 20
x = 8 siswa
Sehingga, banyaknya siswa yang tidak mengikuti ekstrakurikuler pramuka ataupun ekstrakurikuler futsal sebanyak
= 8 orang siswa.
Soal 2.
Di ketahui:
A = { x | 1 < x < 20, maka x merupakan bilangan prima }.
B = { y | 1 y 10, maka y merupakan bilangan ganjil }.
Maka tentukanlah hasil dari A ∩ B ?
Jawab:
A = { 2, 3, 5, 7, 11, 13, 16, 17, 19 }
B = { 1, 3, 5, 7, 9 }
Simbol yang artinya irisan merupakan salah satu cara untuk himpunan anggota yang sama dari himpunan yang saling berhubungan.
A ∩ B = { 3, 5, 7 }
Maka dari itu, hasil dari A ∩ B adalah =
{ 3, 5, 7 }.
Soal 3.
Dari 40 orang bayi, diketahui bahwa terdapat 18 orang bayi yang suka memakan pisang, kemudian ada juga 25 bayi yang suka makan bubur, serta ada juga 9 orang bayi yang menyukai keduanya.
Maka hitunglah berapa banyak bayi yang tidak menyukai pisang dan juga bubur?
Jawab:
n { A Λ B } = ( n { A } + n { B } ) – ( n { S } – n { X } )
9 = ( 18 + 25 ) – ( 40 – n { X } )
9 = 43 – 40 + n { X }
9 = 3 + n { X }
9 – 3 = n { X }
n { X } = 6 orang bayi
Sehingga, banyak bayi yang tidak menyukai pisang dan bubur ada sebanyak
= 6 orang bayi
Demikianlah ulasan singkat mengenai Himpunan Matematika yang dapat kami sampaikan. Semoga ulasan di atas mengenai Himpunan Matematika dapat kalian jadikan sebagai bahan belajar kalian.
The post Himpunan Matematika appeared first on Tuliskan.
ARTIKEL PILIHAN PEMBACA :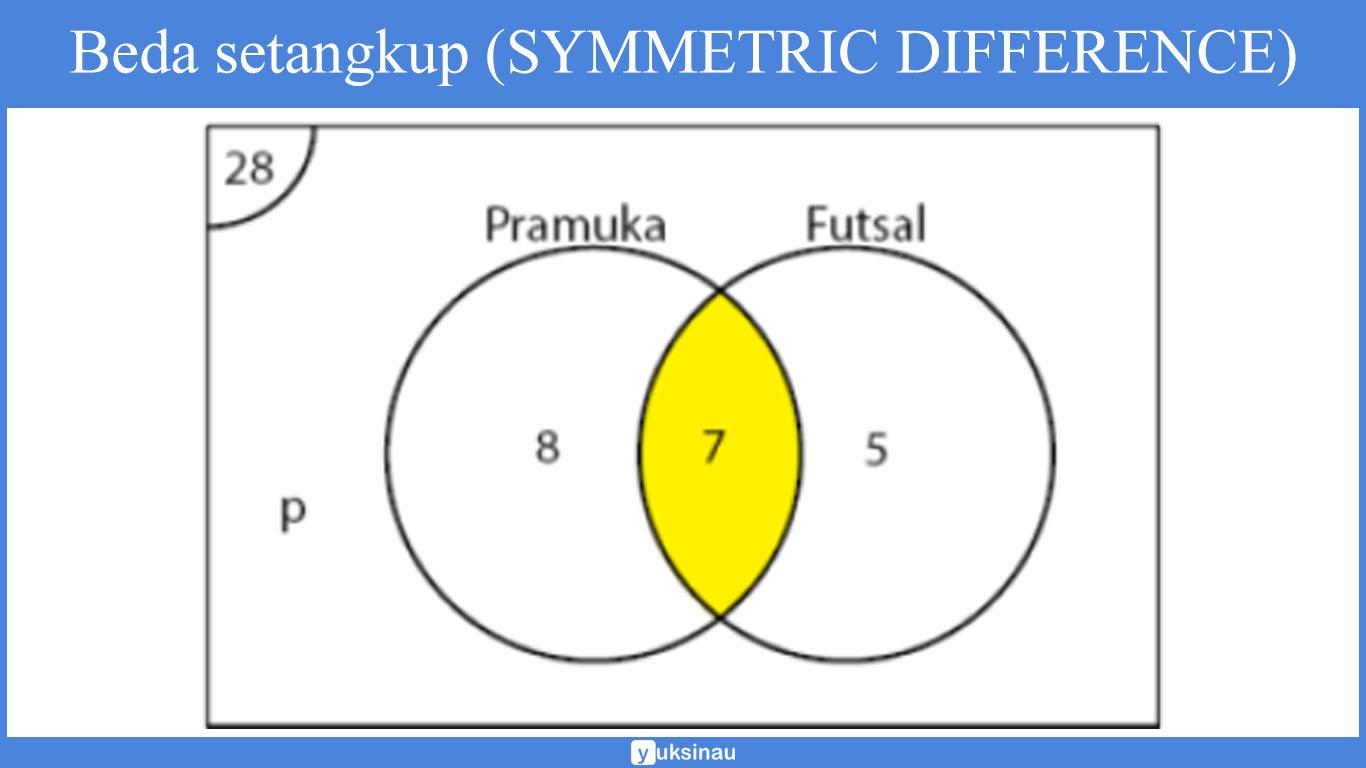
Comments
Post a Comment