Diagram Venn - Poin 100
Keberadaan internet membuat siapa saja bisa mengakses berbagai informasi, maka tidak heran belakangan ini banyak sekali betebaran situs-situs yang membahas mengenai Diagram Venn. Hal ini sangat logis mengingat di era pandemi ini, masyarakat kita lebih sering melakukan proses belajar mengajar secara daring. Baiklah sudah cukup basa-basinya, yuk langsung masuk ke pembahasan saja.
Penjelasan Lengkap Diagram Venn
Saat kalian menduduki bangku kelas 7 SMP, pastinya nanti kalian akan menjumpai adanya materi terkait diagram venn.
Nah, berikut ini akan kami ulasan secara tuntas terkait hal – hal yang berkaitan dengan diagram venn, simak baik – baik ya.
Pengertian Diagram Venn

Diagram venn merupakan suatu diagram yang menampilkan hubungan atau korelasi antar himpunan yang berkesinambungan di dalam sebuah kelompok.
Jenis diagram satu ini dicetuskan oleh seorang ilmuwan asal Inggris yang bernama John Venn.
Dengan menggunakan diagram venn ini, hubungan antar himpunan akan menjadi lebih mudah untuk dipahami.
Pada umumnya, diagram satu ini dipakai untuk menggambarkan suatu himpunan yang saling berpotongan, saling lepas dan seterusnya.
Jenis diagram ini dimanfaatkan untuk penyajian data secara saintifik serta teknik yang bermanfaat di dalam bidang matematika, statistika serta aplikasi komputer.
Himpunan
Himpunan matematika merupakan kumpulan objek yang bisa didefinisikan dengan jelas.
Sebagai contoh pakaian yang tengah kalian kenakan sekarang ini adalah sebuah himpunan, yang di dalamnya termasuk baju, topi, jaket, celana dan yang lainnya.
Kalian bisa menulis adanya sebuah himpunan dengan menggunakan tanda kurung, seperti:
{topi, baju, jaket, celana,…}
Atau kalian juga bisa menulis himpunan di dalam sebuah bilangan, seperti:
Himpunan seluruh bilangan : {0,1,2,3…}
Himpunan bilangan prima: {2,3,5,7,11,13,…}
Diagram venn yang di dalamnya berisi suatu himpunan tadi digambarkan dengan bentuk diagram sehingga mudah untuk dipahami.
Untuk cara menggambarnya, kalian dapat memperhatikan gambar di bawah ini.
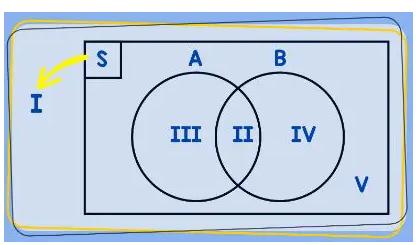
Dari gambar di atas, maka dapat dijelaskan:
I. Himpunan Semesta: Menggambarkan total dari anggota yang dibicarakan.
II. Daerah yang merupakan milik himpunan A dan B (A∩B).
III. Banyak anggota himpunan A saja (tanpa B).
IV. Banyak anggota himpunan B saja (tanpa A).
V. Banyak anggota semesta tetapi bukan anggota A ataupun B.
Aturan Penggambaran Diagram Venn
Untuk membuat suatu diagram venn, maka terdapat beberapa hal yang perlu kalian perhatikan, diantaranya yaitu:
- Himpunan semesta (S) dinyatakan di dalam bentuk persegi panjang. Himpunan semesta merupakan seluruh anggota himpunan yang di dalamnya meliputi himpunan yang tengah menjadi fokus pembahasan.
- Himpunan lain yang menjadi fokus pembahasan telah dinyatakan dengan bentuk lingkaran / kurva tertutup.
- Anggota pada setiap himpunan dinyatakan di dalam bentuk titik / noktah.
- Apabila anggota himpunannya tidak terhingga, maka tiap – tiap anggota tidak perlu untuk dinyatakan sebagai titik.
Supaya lebih jelas, perhatikan contoh di bawah ini:
S = {a, b, c, d, e}
A = {b, d, e}
Diagram venn yang sesuai dengan himpunan di atas yaitu:
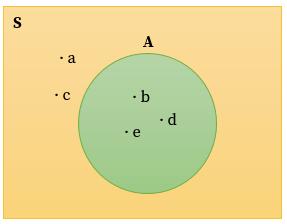
Pada contoh diagram di atas, kalian akan mengenal istilah himpunan bagian, yakni himpunan A adalah himpunan bagian dari himpunan semesta.
Secara matematis maka disimbolkan sebagai A ⊂ S.
Bentuk Diagram Venn
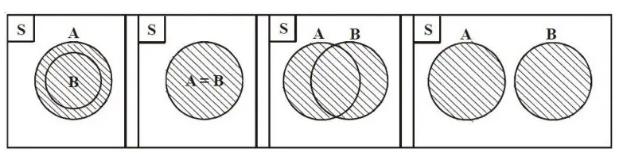
Berikut adalah beberapa bentuk pada diagram venn yang perlu kalian ketahui, antara lain:
1. Himpunan Saling Berpotongan
Diagram satu ini digambarkan dengan dua himpunan yang saling berpotongan sebab memiliki kesamaan.
Sebagai contoh apabila ada himpunan A dan B, keduanya akan saling berpotongan jika memiliki kesamaan maka hal tersebut artinya anggota yang masuk ke dalam himpunan A masuk juga ke dalam himpunan yang B.
Himpunan A yang berpotongan dengan himpunan B dapat ditulis dengan A∩B.
2. Himpunan Saling Lepas
Himpunan A dan B dapat disebut saling lepas apabila anggota himpunan A tidak memiliki anggota yang sama dengan anggota himpunan B.
Himpunan yang saling lepas satu ini bisa kalian tulis dengan A//B.
3. Himpunan Bagian
Himpunan A bisa juga disebut sebagai bagian dari himpunan B jika seluruh anggota himpunan A adalah anggota dari himpunan B.
4. Himpunan yang Sama
Diagram venn jenis menyatakan jika himpunan A serta B terdiri atas anggota himpunan yang sama, sehingga bisa kita simpulkan bahwasannya setiap anggota B adalah anggota A.
Sebagai contoh: A = {2,3,4} dan B= {4,3,2} adalah suatu himpunan yang sama sehingga kalian bisa menulisnya dengan A=B.
5. Himpunan yang Ekuivalen
Himpunan A dan B disebut sebagai ekuivalen jika banyaknya anggota dari kedua himpunan sama.
Himpunan A ekuivalen dengan himpunan B bisa kalian tulis dengan n(A)= n(B).
Di dalam diagram venn ada empat hubungan antar himpunan yang mencangkup irisan, gabungan, komplemen himpunan serta selisih himpunan, berikut penjelasan selengkapnya:
a. Irisan
Irisan himpunan A dan B (A∩B) merupakan suatu himpunan yang mana anggotanya terdapat di dalam himpunan A serta himpunan B.
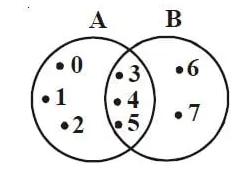
Contoh:
Himpunan A ={ 0,1,2,3,4,5} serta himpunan B ={3,4,5,6,7}.
Perhatikanlah jika diantara kedua himpunan itu ada dua anggota yang sama yakni angka 3,4 dan 5.
Nah, dari kesamaan tersebut dapat disebut bahwa irisan himpunan A dan B dapat ditulis dengan (A∩B) = {3,4,5}.
b. Gabungan
Gabungan himpunan A serta B (ditulis A ∪ B) merupakan suatu himpunan dimana anggotanya adalah himpunan A ataupun anggota himpunan B ataupun anggota dari kedua – duanya.
Gabungan antara himpunan A serta B disimbolkan dengan A ∪ B = {x | x ∈ A atau x ∈ B}
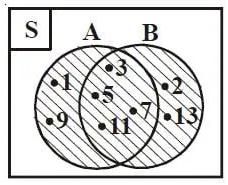
Contoh:
Himpunan A = {1,3,5,7,9,11} serta B= {2,3,5,7,11,13}.
Apabila diantara himpunan A serta himpunan B digabungkan, maka akan membentuk suatu himpunan baru yang anggotanya bisa di tulis menjadi A ∪ B ={1,2,3,5,7,9,11,13}.
c. Komplemen
Komplemen himpunan A (ditulis Ac) merupakan suatu himpunan dimana anggotanya adalah anggota himpunan semesta tetapi bukan anggota himpunan A.
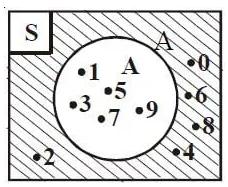
Contoh:
S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} dan A = {1, 3, 5, 7, 9}.
Bisa kalian perhatikan bahwa seluruh anggota S yang bukan dari anggota A membentuk suatu himpunan baru yakni {0,2,4,6,8}.
Sehingga komplemen dari himpunan A yaitu Ac = {0,2,4,6,8}.
Contoh Soal
Untuk memudahkan kalian dalam memahami uraian di atas, berikut kami sajikan contoh soal yang berhubungan dengan diagram venn, antara lain:
1. Dari beberapa anak remaja diketahui ada sebanyak 25 orang yang suka minum susu, 20 orang suka minum kopi serta 12 orang lainnya suka susu dan kopi.
Dari data di atas, jawablah pertanyaan yang ada di bawah ini:
a. Jumlah seluruh anak remaja.
b. Jumlah remaja yang suka susu saja.
c. Jumlah remaja yang suka kopi saja.
d. Jumlah remaja yang suka keduanya.
Jawab:
Untuk bisa menjawab soal di atas, kalian harus membuat data tersebut ke dalam bentuk diagram venn, sehingga gambarnya menjadi:
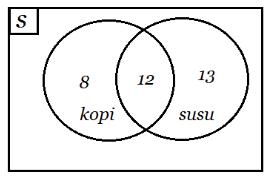
Sehingga diketahui:
a. Jumlah semua anak remaja = 33 orang
b. Jumlah remaja yang suka susu saja = 13 orang
c. Jumlah remaja yang suka kopi saja = 8 orang
d. Jumlah remaja yang suka keduanya = 12 orang
2. Hasil survey pada 35 orang penduduk yang ada di suatu desa, didapatkan hasil sebagai berikut:
- 18 orang menyukai teh
- 17 orang menyukai kopi
- 14 orang menyukai susu
- 8 orang menyukai minum teh dan juga kopi
- 7 orang menyukai teh dan juga susu
- 5 orang menyukai kopi dan juga susu
- 3 orang menyukai ketiga-tiganya.
Gambarlah diagram Venn dari keterangan di atas serta tentukan banyaknya warga yang menyukai teh, menyukai susu, menyukai kopi, serta tidak menyukai ketiganya.
Jawab:
Gambar diagram venn untuk data diatas yaitu:
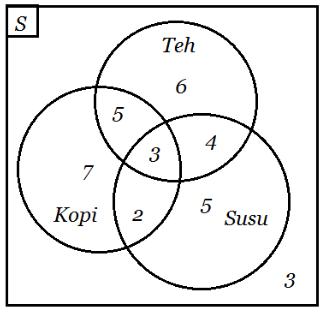
Dari diagram venn diatas, maka diperoleh data:
- Warga yang gemar minum teh saja ada 6 orang.
- Gemar minum susu saja ada 5 orang.
- Gemar minum kopi saja ada 7 orang.
- Serta tidak gemar ketiganya ada 3 orang.
The post Diagram Venn appeared first on Tuliskan.
ARTIKEL PILIHAN PEMBACA :
Comments
Post a Comment